Trajectory optimization and experiment of robotic belt grinding blisk
-
摘要: 整体叶盘具有结构复杂、材料难加工的特点，其加工精度和表面质量对航空发动机整体性能有至关重要的影响。当前，机器人砂带磨削技术已应用于整体叶盘类复杂曲面的磨削加工。然而，在磨削轨迹规划时多采用目标点均布的方式，这就要求目标点必须足够多，从而导致加工效率过低。基于改进的等弦高误差法对整体叶盘机器人砂带磨削的磨削轨迹进行优化分析，并开展相关仿真与实验验证。结果表明：改进的等弦高误差法可根据曲率变化优化磨削轨迹，减少目标加工点数量，从而提高加工效率。经实验验证，与轨迹优化前相比，优化后整体叶盘的加工效率提高了42.9%；优化后的表面粗糙度Ra可达0.26 μm，且叶片一致性较好，尤其是在曲率变化较大的位置。Abstract: The blisk has the characteristics of complex structure and difficult material processing. Its machining accuracy and surface quality have a crucial impact on the overall performance of the aero-engine. At present, the robotic belt grinding has been applied to grinding the complex surface of the blisk. However, since the target points are usually distributed evenly in the grinding trajectory plan, it requires a large amount of points, which leads to low processing efficiency. In this paper, the trajectory is optimized based on the improved equal chord height error method, and relevant simulation and experimental verification are carried out. The results show that the improved equal chord height error method can optimize the grinding trajectory according to the curvature change, reduce the number of target machining points and improve the machining efficiency. Experiments indicate that the machining efficiency of the blisk, compared with that before trajectory optimization, is increased by 42.9%. The surface roughness Ra after optimization can reach 0.26 μm, and the blade consistency is good, especially in the positions where the curvature changes greatly.
-
Key words:
- robot /
- belt grinding /
- blisk /
- trajectory optimization
-
整体叶盘是航空发动机的关键零部件，其制造水平不仅严重影响发动机的推重比，而且还间接反映了一个国家的综合实力。目前，整体叶盘加工制造的主流流程为近成形毛坯制造→精确成形加工→表面抛光[1-2]。一般而言，整体叶盘叶片经精铣加工后仍有明显的铣刀纹路，表面一致性差，需要对其进一步磨削加工以去除铣刀纹路和提高表面完整性。整体叶盘叶片型面为空间自由曲面，结构十分复杂，对精度要求高，加工难度大。手工磨抛仍是整体叶盘的主要精加工方法，存在加工效率低、精度低和表面一致性差等问题[3]，对航空发动机的使用性能和可靠性有着严重的影响。机器人砂带磨削以灵活性高、通用性强和成本低等优势逐渐取代手工磨抛[4]。但合理的轨迹规划一直是复杂曲面机器人砂带磨削加工的难点问题。
为解决以上问题，国内外众多高校和科研院所开始致力于有关机器人砂带磨削轨迹规划的研究。黄云等[5]提出了一种机器人浮动砂带磨削技术，成功应用于钛合金叶片的加工，并满足航发叶片的加工要求。为避免复杂曲面加工时产生的过切问题，XIE等[6]提出了一种基于易磨区域划分的机器人砂带磨削路径生成方法，模仿人工打磨对加工区域进行分区，用截面法对每个易磨区域生成避免过切的路径，有效减少了复杂工件路径生成的复杂性。LV等[7]提出了一种基于材料去除轮廓模型的等残留高度算法，通过考虑接触轮-工件界面的弹性变形来规划刀轨，不仅提高了机器人砂带磨削加工的轮廓精度，而且还解决了叶片前后缘处的过切问题。龙樟等[8]对机器人轨迹规划的研究现状进行了相对全面的综述，分析了现有各种轨迹规划算法的特点，指出了考虑实际工况的多目标最优轨迹规划或将是轨迹规划的一个发展趋势。针对复杂曲面的机器人砂带磨削问题，MA等[9]提出了一种基于曲线长度准则和双三次B样条差值的路径规划方法，可以得到目标点的位置和磨削方向，提高了表面质量。梁子龙等[10]在等残留高度法的基础上提出了改进的Douglas-Peucker算法，可提取抛光刀触点，并解决了自由曲面抛光轨迹规划问题。针对整体叶盘加工中刀具与叶盘易干涉的问题，WANG等[11]提出了一种可检测碰撞和避免干涉的算法，可实现在调整刀具姿态时保证工件的表面质量。CUI等[12]提出了一种抑制空间柔性机械臂振动的轨迹规划方法，利用粒子群优化算法求出轨迹规划的最优解。张铁等[13]在机器人磨削离线编程系统上进行了机器人磨削路径插补算法的研究，提出了一种改进的泰勒插补算法，该算法可根据加工路径的曲率变化自适应地增减刀位点，从而保证加工效率。WANG等[14]基于鲸鱼优化算法和差分进化算法提出了一种改进的鲸鱼优化算法，实现了磨削机器人的最优轨迹规划。
综上所述，针对不同的加工对象，众多学者提出了不同的技术或算法来实现机器人的最优轨迹规划。虽然他们所加工的对象也是复杂曲面，但很少有类似整体叶盘结构的工件，也很少有涉及整体叶盘机器人砂带磨削轨迹规划的研究。因此，结合整体叶盘的加工难点和机器人砂带磨削的特点，对整体叶盘的机器人砂带磨削轨迹进行优化分析，提出了一种改进的变曲率等弦高误差法，并开展了相关仿真和实验验证。
1. 整体叶盘机器人砂带磨削轨迹优化
不同于人工打磨，机器人砂带磨削的特点是使用机器人和砂带磨头对复杂曲面零件进行灵活磨削加工。为保证最终的表面质量和加工效率，机器人砂带磨削不仅需要对磨削压力和磨头姿态进行准确控制，而且还需要考虑砂带线速度和轨迹规划等加工参数的影响。
机器人砂带磨削的运动轨迹是指砂带磨头依次走完所规划的刀位点的连续路径。在进行机器人砂带磨削的轨迹规划时，需要解决的问题主要包括：（1）确定合适的走刀方式；（2）确定合适的加工步长控制方法；（3）确定合适的加工行距控制方法；（4）在轨迹规划的同时避免加工干涉问题。
为使叶片型面满足流体动力学要求，一般将整体叶盘叶片型面设计为复杂的自由曲面。目前，自由曲面定义和表达最强大的是非均匀有理B样条曲面（NURBS曲面）。NURBS曲面的数学表达形式[15]为
$$ P(u,v) = \dfrac{{\displaystyle\sum\limits_{i = 0}^m {\displaystyle\sum\limits_{j = 0}^n {{w_{ij}}{P_{ij}}{N_{ip}}(u){N_{jq}}(v)} } }}{{\displaystyle\sum\limits_{i = 0}^m {\displaystyle\sum\limits_{j = 0}^n {{w_{ij}}{N_{ip}}(u){N_{jq}}(v)} } }}， {\text{ }}u,v \in [0,1] $$ (1) 其中：
${w_{ij}}$ 是控制顶点的权值，${P_{ij}}$ 是控制顶点，${N_{ip}}$ 表示u向上第i个p次B样条基函数，${N_{jq}}$ 表示v向上第j个q次B样条基函数。显然，当式（1）中的u或v其中一个参数确定时，便可得到一条NURBS曲线。例如，令
$v = {v_0}$ （${v_0}$ 为常数），则u向NURBS曲线的数学表达式为$$ P(u) = P(u,{v_0}) = \dfrac{{\displaystyle\sum\limits_{i = 0}^m {\displaystyle\sum\limits_{j = 0}^n {{w_{ij}}{P_{ij}}{N_{ip}}(u){N_{jq}}({v_0})} } }}{{\displaystyle\sum\limits_{i = 0}^m {\displaystyle\sum\limits_{j = 0}^n {{w_{ij}}{N_{ip}}(u){N_{jq}}({v_0})} } }}{\text{ = }}\dfrac{{\displaystyle\sum\limits_{i = 0}^n {{w_i}{P_i}{N_{ip}}(u)} }}{{\displaystyle\sum\limits_{i = 0}^n {{w_i}{N_{ip}}(u)} }} $$ (2) NURBS曲线在曲面上某点
${P_0}({u_0},{v_0})$ 沿u、v参数线方向的切矢量为$$ {{\boldsymbol{P}}_u}({u_0},{v_0}) = \dfrac{{\partial P}}{{\partial u}}{\Bigg|_{({u_0},{v_0})}},{{\boldsymbol{P}}_v}({u_0},{v_0}) = \dfrac{{\partial P}}{{\partial v}}{\Bigg|_{({u_0},{v_0})}} $$ (3) 式（3）对参数u进行求导，可以得到曲线的一阶导数为
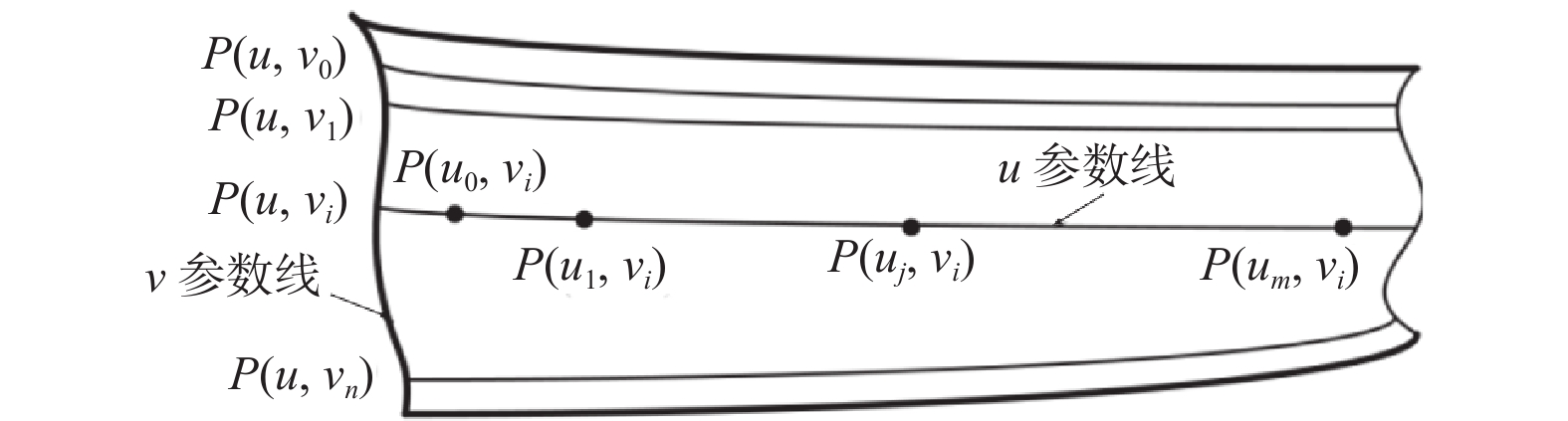
$$ P'(u) = \dfrac{{\displaystyle\sum\limits_{i = 0}^n {{w_i}{P_i}N{'_{ip}}(u)} - \displaystyle\sum\limits_{i = 0}^n {{w_i}N{'_{ip}}(u)} \dfrac{{\displaystyle\sum\limits_{i = 0}^n {{w_i}{P_i}{N_{ip}}(u)} }}{{\displaystyle\sum\limits_{i = 0}^n {{w_i}{N_{ip}}(u)} }}}}{{\displaystyle\sum\limits_{i = 0}^n {{w_i}{N_{ip}}} }} $$ (4) 在整体叶盘机器人砂带磨削加工中，被砂带包裹的接触轮和整体叶盘叶片间主要包含沿步长方向的走刀运动和沿行距方向的进给运动2种相对运动。为便于解释，假定步长方向为曲面的u参数线方向，行距方向为曲面的v参数线方向。如图1所示，轨迹规划的任务可被分为2部分：（1）根据叶片表面形状确定
${v_i}(i = $ $ 0,1,2, \cdot \cdot \cdot ,n)$ 的值，得到一系列u参数线；（2）在所确定的u参数线上确定${u_j}(j = 0,1,2, \cdot \cdot \cdot ,m)$ 的值，得到一系列加工目标点$P({u_j},{v_i})$ 的位置。
图 1 整体叶盘叶片型面砂带磨削轨迹离散示意图Figure 1. Diagram of trajectory discrete for belt grinding of blisk blade机器人砂带磨削路径轨迹规划方法的核心在于如何确定磨削轨迹的走刀步长与加工行距。走刀步长一般采用等弦高误差法进行计算，而加工行距多采用等残留高度法进行计算。然而，这2种算法都需要一个前提：假定相邻2个加工目标点的曲率大体相同。而实际在计算走刀步长的过程中，当2个相邻目标点的曲率相差较大时，易出现所规划的轨迹过于稀疏从而影响加工质量的情况。因此，为提高整体叶盘表面的加工质量，需要对计算走刀步长所采用的等弦高误差法进行优化，提出一种改进的变曲率等弦高误差法。
如图2所示，定义L为加工步长，Ai和Ai+1分别为路径上的2个目标点，
${R_i}$ 和${R_{i + 1}}$ 分别为2个目标点的曲率半径，O1和O2分别为2个目标点位置接触轮的中心点，$\delta '$ 为实际弦高误差，$\delta $ 为允许的加工误差。
图 2 变曲率等弦高误差计算示意图Figure 2. Calculation schematic diagram of constant chord height error with variable curvature当磨削路径上的相邻目标点曲率相差不大时，可假定
$R = {R_i} = {R_{i + 1}}$ 。显然，由图2中的几何关系可知：$$ {R^2} = {(R - \delta ')^2} + {(L/2)^2},\delta ' \leqslant \delta $$ (5) 但当相邻目标点的曲率相差较大时，不能认为其曲率近似相等，应综合对比，取其中较大者作为式（5）中的曲率R，即
$$ R = \left\{ {\begin{array}{l} {\dfrac{1}{{{\rho _i}}}，{\text{ }}{\rho _i} \geqslant {\rho _{i + 1}}} \\ {\dfrac{1}{{{\rho _{i + 1}}}}，{\text{ }}{\rho _i} < {\rho _{i + 1}}} \end{array}} \right. $$ (6) 其中，
${\rho _i}$ 和${\rho _{i + 1}}$ 分别为相邻2个目标点处的曲率。由式（5）可知，加工步长的计算公式为
$$ L \leqslant \sqrt {8\delta R} $$ (7) 由于整体叶盘叶片磨削的轨迹较为密集，为简化计算，假设2个目标点间的曲线弧长与加工步长相同，即
$\wideparen {{{A}_{i}}{{A}}}_{i+1}=L$ ，则：$$\wideparen{{{A}_{i}}{{A}}}_{i+1}=L=\int_{{{u}_{i}}}^{{{u}_{i+1}}}{P'(u){\rm{d}}u}$$ (8) 将式（7）和当前点的
${u_i}$ 值代入式（8）可求出该条磨削路径对应的下个目标点的${u_{i + 1}}$ 值，通过该计算方法的不断迭代，便可求出该条磨削路径上各个目标点对应的参数值。2. 整体叶盘机器人砂带磨削加工仿真
整体叶盘结构复杂，总体加工耗时长，而砂带磨头具有一定的柔性，加工调试过程较易发生干涉。因此有必要借助仿真软件提前对整体叶盘砂带磨削加工程序进行仿真分析，以实现整体叶盘加工的快速验证。选用ABB机器人专用的仿真软件RobotStudio作为仿真实验平台。
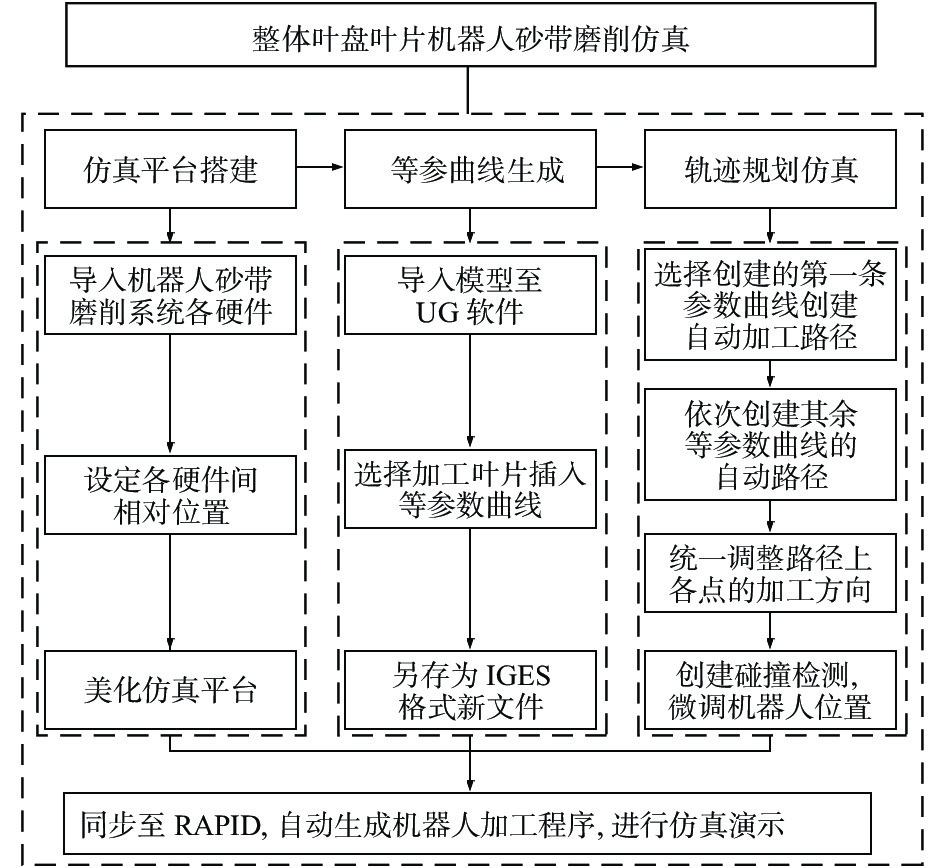
整体叶盘机器人砂带磨削仿真流程主要包含仿真平台搭建、等参数曲线生成和轨迹规划仿真等3部分，如图3所示。其中，仿真平台搭建用于设定整体叶盘相对于机器人基坐标系的位置信息；等参数曲线生成用于重构获取整体叶盘叶片表面的u或v参数线；轨迹规划用于在设定的路径上自动生成目标加工点。
图 3 整体叶盘叶片机器人砂带磨削仿真流程图Figure 3. Flow chart of simulating blisk grinding with robotic belt2.1 仿真平台搭建
机器人砂带磨削系统主要包含的硬件有ABB IRB4600-60/2.05机器人、控制柜、砂带磨头装置（含砂带磨头夹具和砂带磨头）、叶盘专用夹具和数控转台。在进行仿真平台搭建时，为保证仿真加工的真实性和有效性，应使仿真软件内搭建的仿真平台与实际的机器人砂带磨削系统尽量保持一致。其中，最关键的数据为整体叶盘相对于机器人坐标系原点的位置信息和砂带磨头相对于机器人末端TCP中心的位置信息。
在搭建仿真平台时，机器人和控制柜可从仿真软件内直接导入。为方便制图，砂带磨头装置、叶盘专用夹具、数控转台和整体叶盘需要从外部导入（支持导入STEP或IGES格式的三维模型）。硬件模型导入仿真软件后，需要根据实际的情况准确设定各个硬件的位置。为实现机器人末端与砂带磨头的一致运动，必须将砂带磨头安装于机器人末端。搭建完成的仿真平台如图4所示。
2.2 自动路径创建
在生成整体叶盘表面等参曲线和建立好加工环境后，可在仿真软件内自动生成加工轨迹，设定磨头与机器人之间的碰撞检测，并根据具体的干涉或碰撞情况微调机器人的姿态使其正常运行所规划的加工轨迹。
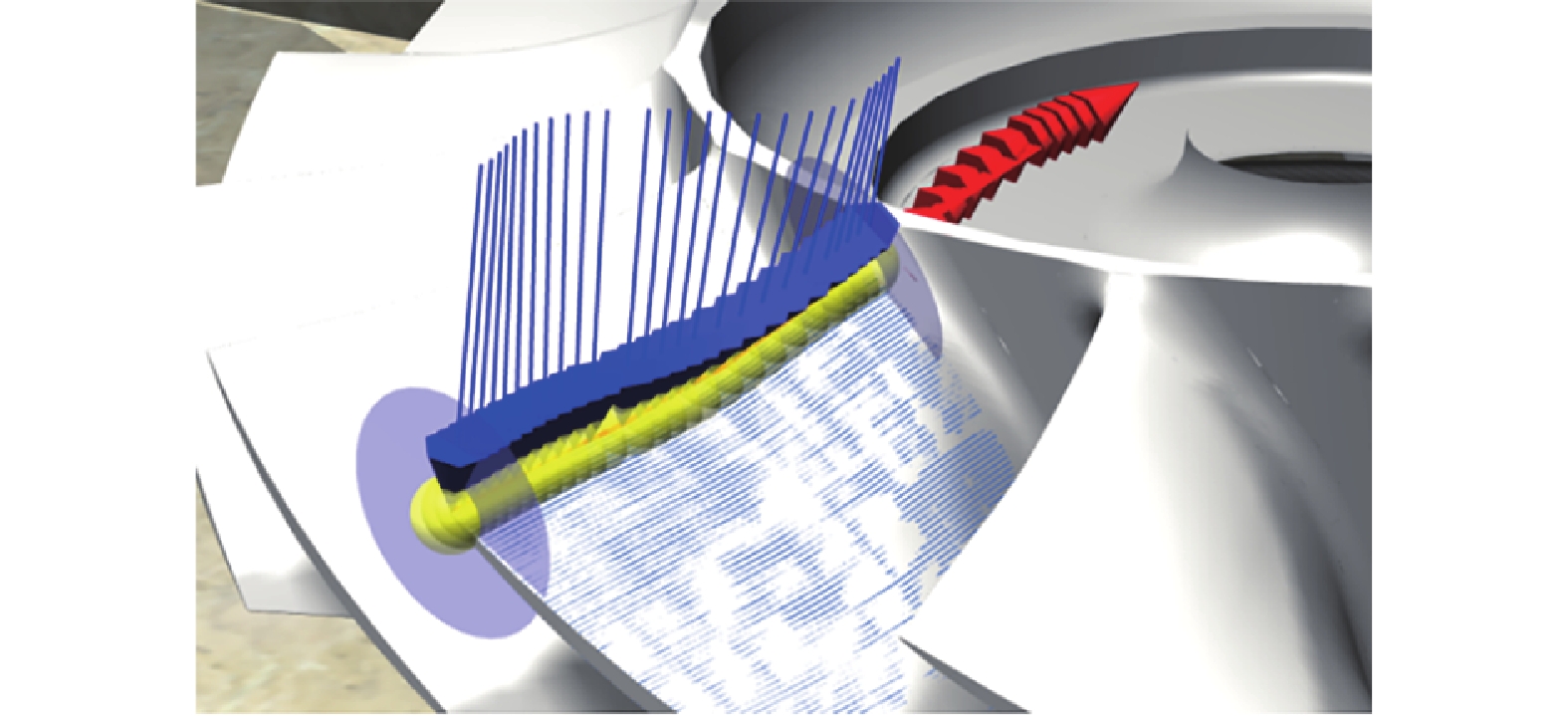
为自动生成加工路径点，在仿真软件内选择“自动路径”，在弹出的窗口中先选择某一待加工叶片曲面作为参照面，然后选择曲面上的若干等参曲线作为自动路径创建一系列目标点，同时设置目标点的公差等参数。某一路径生成的目标点如图5所示。
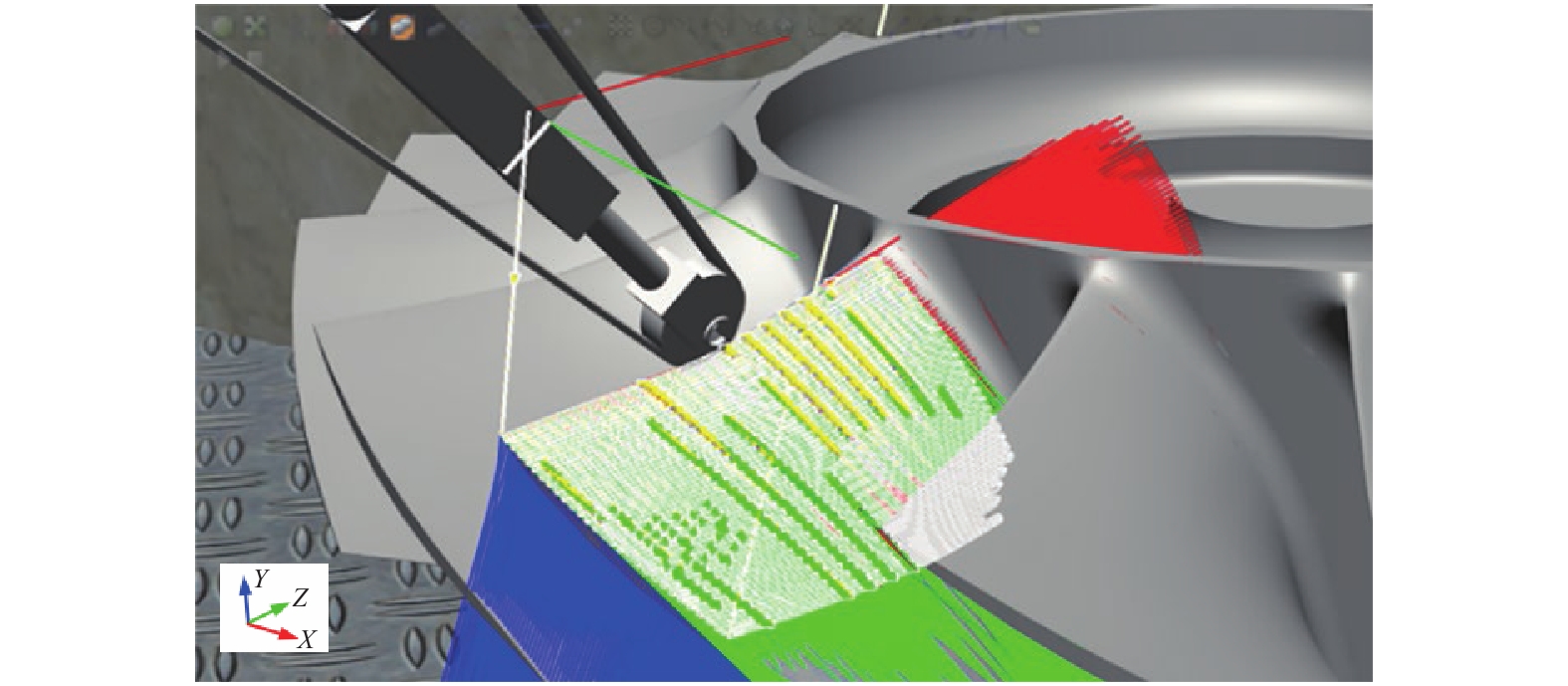
使用软件的自动路径功能自动生成加工目标点时，要注意保证相邻2条路径的加工方向一致。为保证加工过程的连续，始终保持目标加工点的X轴沿曲线切向并指向轮毂方向，Z轴垂直于曲线切向并指向叶背方向，Y轴由右手定则确定。当出现与上述规定的加工点方向不同的情况时，可使其绕本地坐标进行一定的旋转调整至规定方向。调整过后的加工轨迹如图6所示。
2.3 碰撞检测与仿真
为监测机器人各轴与砂带磨头的干涉情况，可设定碰撞检测。利用软件的仿真功能自动创建碰撞检测，设定机器人与砂带磨头碰撞时显示红色，距离10 mm以内时显示黄色。结合在碰撞检测中所观察到的碰撞位姿和即将碰撞的位姿，通过重定位微调修改机器人的位姿以实现无碰撞无干涉加工。
将加工目标点添加到路径后，选择“同步到RAPID”，并注意同步工件坐标和工具坐标的相关信息，随后可进行轨迹规划的仿真演示，演示结果如图7所示。
3. 整体叶盘机器人磨削实验
3.1 实验材料
本实验的对象为某航空发动机的整体叶盘，材质为钛合金材料，部分结构如图8所示。
3.2 实验装置
本实验所采用的机器人砂带磨削实验平台主要由机器人、机器人控制柜、砂带磨头装置（含砂带磨头夹具和砂带磨头）、叶盘专用夹具和数控转台等组成，如图9所示。
在此实验平台中，机器人采用ABB公司生产的IRB4600-60/2.05型机器人，机器人末端与砂带磨头通过气动砂带磨头夹具连接，整体叶盘工件与数控转台通过叶盘专用夹具连接，机器人控制柜与PC通过双绞线连接。其中，砂带磨头为重庆三磨海达磨床有限公司生产的数控专用砂带磨头，转速可实时调整，且磨头具有一定的浮动功能。数控转台采用Detron公司生产的GFA255H型五轴数控转台，可实现对工件的精确分度。
3.3 实验过程
（1） 进行如图7所示的整体叶盘加工离线仿真，检查在加工过程中是否出现加工干涉现象，若无干涉现象，则将加工程序通过双绞线在线导入机器人控制器，准备现场加工。
（2） 配置机器人与磨头、转台通信，实现通过示教器控制磨头转停、转速调节及转台转停，分别导入轨迹优化前后的2个机器人加工程序。
（3） 进行整体叶盘的预磨削实验。关闭砂带磨头开关，通过示教器运行加工程序，观察机器人末端砂带磨头的位姿是否正确。若有干涉的问题，则重新生成加工程序；若正确无误，则打开砂带磨头开关，正式进行整体叶盘磨削实验。在机器人磨削加工过程中，工艺参数设置如表1所示。
表 1 机器人砂带磨削加工工艺参数设置Table 1. Parameter setting of robotic belt grinding process砂带类型 砂带粒度代号 线速度vw / (m·s−1) 进给速度vt / (mm·s−1) 金刚石 P200 10 20 （4） 当完成1个叶片的加工后，转动转台继续加工下个叶片。由于待加工的整体叶盘共有11个叶片，所以应控制数控转台带动整体叶盘转动32.727°。依次类推可完成整个叶盘的加工。
（5） 分别记录轨迹优化前后2个程序机器人砂带磨削单个叶片所耗费的时间。卸下磨削完成的整体叶盘，分别测量其表面形貌和粗糙度。
4. 实验结果分析
（1）整体叶盘轨迹优化前后的对比如图10所示。在整体叶盘加工仿真中，对比分析使用轨迹优化算法前后某一磨削路径的加工目标点，如图10a和图10c所示，可看出优化后的磨削路径上的磨削点数量减少，且会随曲率的变化而调整，这主要是因为轨迹优化算法在保证精度的同时，尽量减少了目标点数量以提高加工效率。
图 10 整体叶盘轨迹优化前后对比图Figure 10. Comparison diagram before and after trajectory optimization of blisk经整体叶盘磨削实验后，可看出优化前后表面质量整体相差不多，如图10b和图10d所示，但优化后的表面一致性略好。经轨迹优化，整体叶盘机器人砂带磨削单个叶片的磨削时间由原来的20 min缩短为14 min，整体叶盘的加工效率提高了42.9%。磨削时间的缩短主要是因为采用轨迹优化算法减少了加工目标点的数量，从而缩短了加工用时，这正反映了轨迹优化算法的优势。
（2）采用便携式显微镜对轨迹优化前后的表面形貌进行放大观察。轨迹优化前后对比效果如图11所示。通过对比可以发现：轨迹优化前后的表面质量相差不大，但轨迹优化后的表面纹理更加均匀一致。这主要是因为轨迹优化算法考虑了部分位置曲率较大的情况。
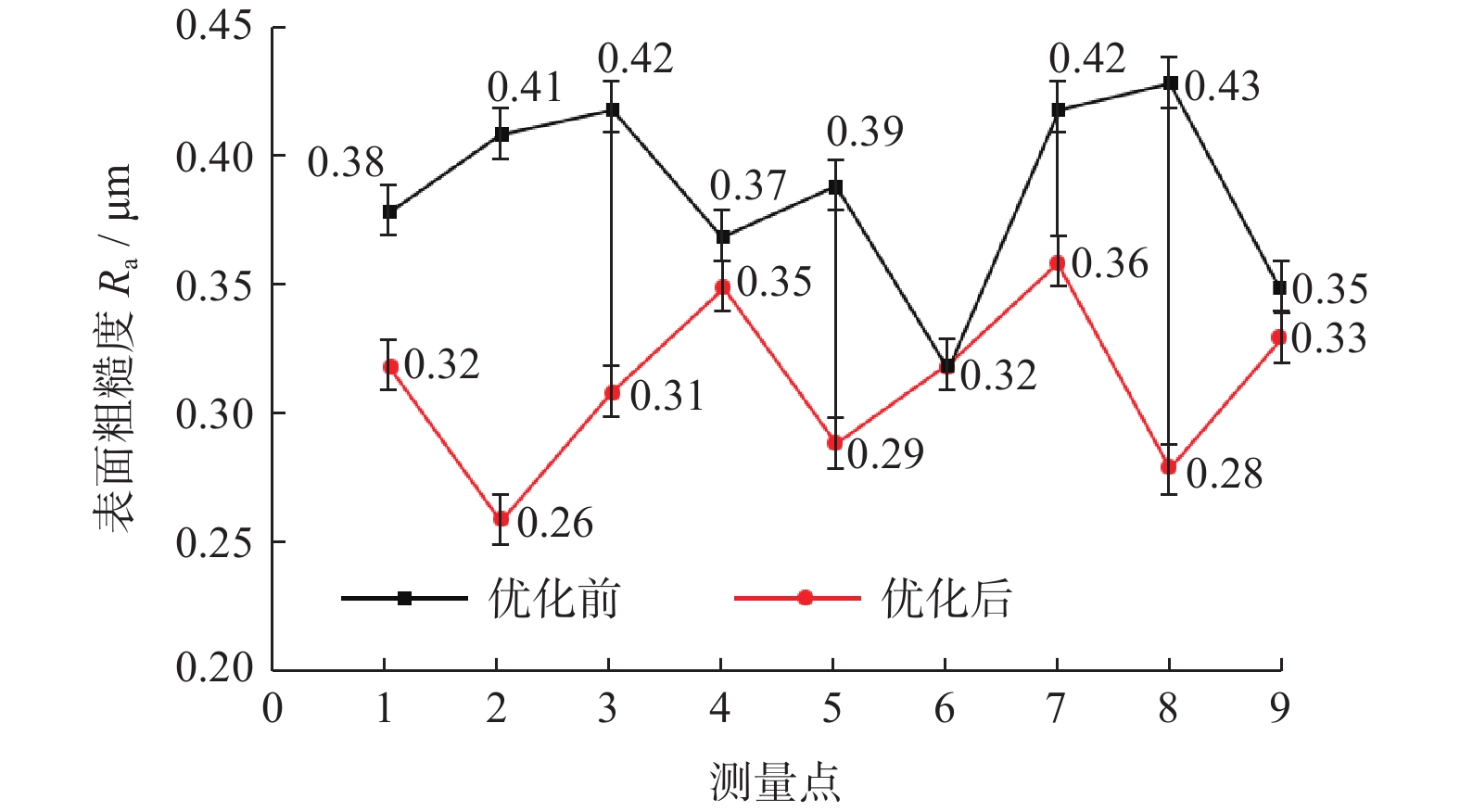
（3）采用英国Taylor-Hobson公司生产的型号为Form Talysurf Series表面轮廓仪进行表面粗糙度测量。本实验在整体叶盘的相邻2个叶片上分别选取9个测量点位，如图12所示，测得轨迹优化前后的粗糙度值，测量结果如图13所示。
图 11 轨迹优化前后表面形貌对比图Figure 11. Comparison of surface morphology before and after trajectory optimization
图 12 整体叶盘叶片粗糙度测量点分布图Figure 12. Distribution map of roughness measurement points on blisk blade
图 13 整体叶盘叶片轨迹优化前后表面粗糙度对比Figure 13. Comparison of surface roughness before and after trajectory optimization for blisk blade从图13中可以看出：轨迹优化前的表面粗糙度大多在Ra=0.38 μm左右，而优化后叶片表面粗糙度Ra都在0.36 μm以下，最小粗糙度Ra为0.26 μm，普遍比优化前的粗糙度更小。出现这种情况的原因主要是采用轨迹优化算法可以根据曲率的变化情况调整2目标点间的距离；相比目标点均布的轨迹，目标点距离不等的轨迹更符合曲线的特征，从而改善其表面质量。
5. 结论
对整体叶盘机器人砂带磨削的磨削轨迹进行了优化分析，并开展了相关仿真和实验验证。所得的结论如下：
（1）基于变曲率等弦高误差法的机器人砂带磨削轨迹优化方法可提高加工效率，单个叶片的打磨时间由优化前的20 min缩短为14 min，整体叶盘的加工效率提高了42.9%。
（2）优化后的磨削轨迹可提高航空发动机整体叶盘的表面质量，有效去除了铣削纹路。
（3）优化后的表面粗糙度和一致性较好，都在Ra 0.36 μm以下，最小可达Ra 0.26 μm，尤其是在曲面曲率变化较大位置处，能满足整体叶盘叶片的加工要求。
-
图 1 整体叶盘叶片型面砂带磨削轨迹离散示意图
Figure 1. Diagram of trajectory discrete for belt grinding of blisk blade
图 2 变曲率等弦高误差计算示意图
Figure 2. Calculation schematic diagram of constant chord height error with variable curvature
图 3 整体叶盘叶片机器人砂带磨削仿真流程图
Figure 3. Flow chart of simulating blisk grinding with robotic belt
图 10 整体叶盘轨迹优化前后对比图
Figure 10. Comparison diagram before and after trajectory optimization of blisk
图 11 轨迹优化前后表面形貌对比图
Figure 11. Comparison of surface morphology before and after trajectory optimization
图 12 整体叶盘叶片粗糙度测量点分布图
Figure 12. Distribution map of roughness measurement points on blisk blade
图 13 整体叶盘叶片轨迹优化前后表面粗糙度对比
Figure 13. Comparison of surface roughness before and after trajectory optimization for blisk blade
表 1 机器人砂带磨削加工工艺参数设置
Table 1. Parameter setting of robotic belt grinding process
砂带类型 砂带粒度代号 线速度vw / (m·s−1) 进给速度vt / (mm·s−1) 金刚石 P200 10 20 
下载: 导出CSV
-
[1] 黄云, 肖贵坚, 邹莱. 航空发动机叶片机器人精密砂带磨削研究现状及发展趋势 [J]. 航空学报,2019,40(3):53-72.HUANG Yun, XIAO Guijian, ZOU Lai. Current situation and development trend of robot precise belt grinding for aero-engine blade [J]. Acta Aeronautica et Astronautica Sinica,2019,40(3):53-72. [2] 陈霖. 航空发动机整体叶盘机器人磨抛工艺与参数优化 [D]. 武汉: 华中科技大学, 2020.CHEN Lin. Robotic blisk grinding process and parameter optimization for aero engine [D]. Wuhan: Huazhong University of Science and Technology, 2020. [3] 刘秀梅, 肖贵坚, 刘智武, 等. 航空发动机整体叶盘数控砂带磨削变形行为及其试验研究 [J]. 金刚石与磨料磨具工程,2020,40(3):25-32. doi: 10.13394/j.cnki.jgszz.2020.3.0004LIU Xiumei, XIAO Guijian, LIU Zhiwu, et al. Research on deformation behavior of NC belt grinding of aero-engine blisk and its test [J]. Diamond & Abrasives Engineering,2020,40(3):25-32. doi: 10.13394/j.cnki.jgszz.2020.3.0004 [4] SONG Y X, YANG H J, LV H B. Intelligent control for a robot belt grinding system [J]. IEEE Transactions on Control Systems Technology,2013,21(3):716-724. doi: 10.1109/TCST.2012.2191587 [5] 黄云, 侯明明, 刘阳, 等. 航空发动机钛合金叶片机器人浮动砂带磨削技术及其试验研究 [J]. 航空制造技术,2020,63(5):14-19. doi: 10.16080/j.issn1671-833x.2020.05.014HUANG Yun, HOU Mingming, LIU Yang, et al. Robotic floating belt grinding technology and experimental study on aero-engine titanium alloy blade [J]. Aeronautical Manufacturing Technology,2020,63(5):14-19. doi: 10.16080/j.issn1671-833x.2020.05.014 [6] XIE H L, LI J R, LIAO Z Y, et al. A robotic belt grinding approach based on easy-to-grind region partitioning [J]. Journal of Manufacturing Processes,2020,56(8):830-844. doi: 10.1016/j.jmapro.2020.03.051 [7] LV Y J, PENG Z, QU C, et al. An adaptive trajectory planning algorithm for robotic belt grinding of blade leading and trailing edges based on material removal profile model [J]. Robotics and Computer-Integrated Manufacturing,2020,66:101987. doi: 10.1016/j.rcim.2020.101987 [8] 龙樟, 李显涛, 帅涛, 等. 工业机器人轨迹规划研究现状综述 [J]. 机械科学与技术,2021,40(6):853-862. doi: 10.13433/j.cnki.1003-8728.20200132LONG Zhang, LI Xiantao, SHUAI Tao, et al. Review of research state of trajectory planning for industrial robots [J]. Mechanical Science and Technology for Aerospace Engineering,2021,40(6):853-862. doi: 10.13433/j.cnki.1003-8728.20200132 [9] MA K W, HAN L, SUN X X, et al. A path planning method of robotic belt grinding for workpieces with complex surfaces [J]. IEEE/ASME Transactions on Mechatronics,2020,25(2):728-738. doi: 10.1109/TMECH.2020.2974925 [10] 梁子龙, 丁毓峰. 一种自由曲面抛光机器人轨迹规划方法 [J]. 机械科学与技术,2018,37(10):1489-1495. doi: 10.13433/j.cnki.1003-8728.20180071LIANG Zilong, DING Yufeng. A trajectory planning method for free-form surface polishing robot [J]. Mechanical Science and Technology for Aerospace Engineering,2018,37(10):1489-1495. doi: 10.13433/j.cnki.1003-8728.20180071 [11] WANG Y M, YANG J X, LI D W, et al. Tool path generation with global interference avoidance for the robotic polishing of blisks [J]. The International Journal of Advanced Manufacturing Technology, 2021, 117(3/4): 1223-1232. [12] CUI L L, WANG H S, CHEN W D. Trajectory planning of a spatial flexible manipulator for vibration suppression [J]. Robotics and Autonomous Systems,2020,123:1-11. doi: 10.1016/j.robot.2019.103316 [13] 张铁, 张斌. 机器人砂带磨削路径优化插补算法 [J]. 中国机械工程,2018,29(8):983-990.ZHANG Tie, ZHANG Bin. Optimized interpolation algorithm for robotic belt grinding processes [J]. China Mechanical Engineering,2018,29(8):983-990. [14] WANG T, XIN Z J, MIAO H B, et al. Optimal trajectory planning of grinding robot based on improved whale optimization algorithm [J]. Mathematical Problems in Engineering,2020(4):1-8. doi: 10.1155/2020/3424313 [15] 徐立国, 孙瑞东, 党敬民. 可变阶数NURBS曲面的相机标定模型 [J]. 农业机械学报,2020,51(8):420-426. doi: 10.6041/j.issn.1000-1298.2020.08.048XU Liguo, SUN Ruidong, DANG Jingmin. Variable order NURBS surface model for camera calibration [J]. Transactions of the Chinese Society for Agricultural Machinery,2020,51(8):420-426. doi: 10.6041/j.issn.1000-1298.2020.08.048 期刊类型引用(3)
1. 王小东，杨骞，程圣，朱正清. 航发叶片磨抛工艺分析与经济性评价. 制造技术与机床. 2024(08): 26-31 . 
百度学术2. 孙梓洲，陈付磊，胡皓，戴一帆，关朝亮，彭小强. 高精度光学元件控时磨削方法研究. 中国科学:技术科学. 2023(08): 1302-1312 . 百度学术3. 李文辉，温学杰，李秀红，张演. 整体叶盘抛磨技术研究现状及其发展趋势. 航空制造技术. 2022(17): 88-102 . 百度学术其他类型引用(3)
-
下载:
百度学术
点击查看大图
计量
- 文章访问数: 1042
- HTML全文浏览量: 455
- PDF下载量: 61
- 被引次数: 6
邮件订阅
RSS
