On-line identification and monitoring method for external grinding flutter based on BP neural network
-
摘要: 为提高机床磨削加工过程中对颤振现象识别的能力,提出一种基于BP(back propagation)神经网络模型的颤振识别方法。通过对加工过程中传感器采集到的高频声发射信号以及振动信号相关特征值的提取,获得关于颤振的多特征参数样本库,并用其对BP神经网络模型进行学习和训练,建立BP神经网络在线识别颤振的算法模型,实现对机床加工过程中是否发生颤振的在线监测和识别。试验结果表明:这种基于BP神经网络模型的颤振识别测试结果与磨削加工试验中的磨削颤振现象结果相符合。该方法能够有效地识别磨削加工过程中的颤振,并起到在线监测识别的作用。Abstract: To improve the ability of the machine tool to identify chatter during the grinding process, a chatter recognition method is proposed based on the BP (back propagation) neural network model. By extracting the relevant feature values of the high-frequency acoustic emission signals and vibration signals in the processing process, multi-feature signal samples library about flutter are obtained. The multi-feature signal sample library is used to learn and train the BP neural network to establish recognition model. The model realizes on-line monitoring and accurate identification of whether chattering occurring during machine tool processing. The experimental results show that the flutter recognition based on the BP neural network model verifies that the measured test results are consistent with the actual flutter and network recognition results. Therefore, this method can effectively identify the flutter phenomenon in the processing process and play the role of online intelligent monitoring.
-
磨削是一种在精度要求较高时去除工件表面材料的机械加工方法,而颤振是磨削过程中影响加工质量的关键因素[1]。工件的几何误差、尺寸误差、表面粗糙度等指标的恶化都可能是颤振所导致[2]。颤振的产生不可控,且机理复杂,从根源上对其分析有一定的盲目性和局限性[2]。因此,针对外圆磨削颤振现象进行在线监测及识别,做出工艺调整[1],对改善工件表面质量、提高加工效率具有重要意义。
近年来,国内外学者对颤振监测做了许多研究,并通过“脱机操作”对工件表面进行光学测量来提高效率。于骏一等[3]在切削颤振发生之前对颤振进行了预报。孔繁森等[4]利用模糊数学原理将理论信号与试验数据做贴合度分析进而进行了颤振识别。钱士才等[5]通过支持向量机对颤振进行了识别。这些方法有一定的效果,但是传感器信号太单一,数据、特征参数少。吕长飞等[6]通过幅值法和小波分析实现了颤振的预测,但是小波分析局限于信号低频部分,而且没有深入考虑算法模型与数据适配问题,对结果的准确性影响较大。
KULJANIC等[7]利用神经网络对多颤振特征进行了信息融合、学习训练和分类识别。为研究在磨削加工的复杂条件下的加工颤振现象,利用能够以任意精度逼近非线性连续函数的BP神经网络模型,实现从输入到输出的映射,特别适用于求解这种内部机制复杂的问题。多传感器作用下的BP神经网络模型也拥有高度自学习和自适应的能力,在对机床磨削颤振进行在线监测和识别时,主要通过对高频声发射传感器信号、三向振动传感器采集到的原始信号进行时域特征参数和小波包特征参数的提取,建立多样本数据库,对算法模型进行反复训练得出识别结果,实现对机床磨削颤振现象的在线监测及识别。
1. 颤振机理与监测
金属加工过程中的振动分为强迫振动和自激振动[8]。强迫振动是受到的系统外周期性的扰动。刀具和工件在加工过程没有周期性外力作用也会产生强烈的相对振动,该振动称为自激振动,也称颤振[9]。
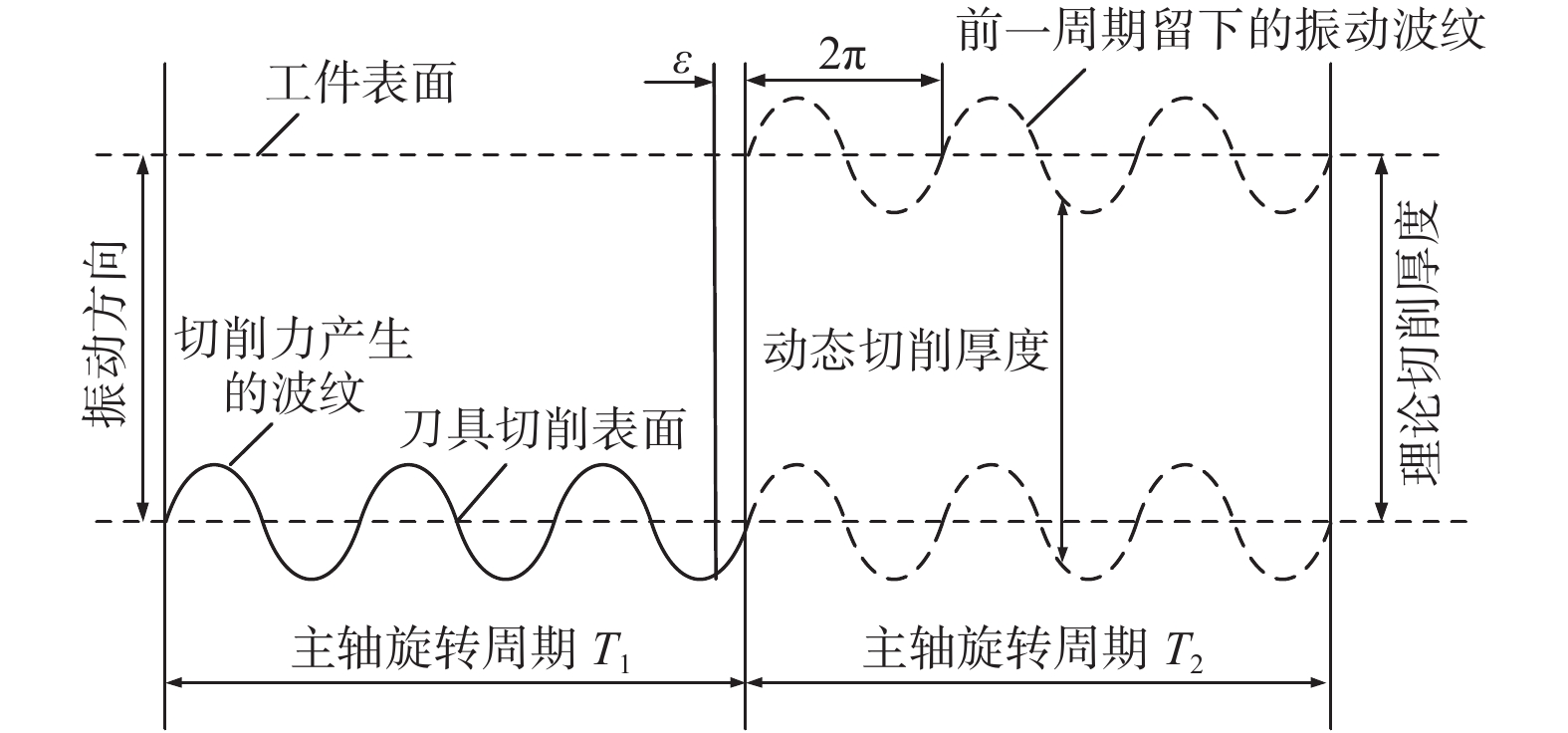
再生型颤振是自激振动的一种,几乎在所有的机床加工中都有发生。其产生机理是由于上次切削所形成的振纹与本次切削的振动位移之间产生了一定的相位差,动态切削厚度发生变化。当厚度达到一定程度时,就会发生再生型颤振。
如图1所示,当连续2次磨削产生振纹的相位差ε为0或2π时,动态切削厚度都不会发生变化;当相位差为π时,动态切削厚度变化到最大值,颤振也最严重。由于振源来自机床内部,即使严格选取工艺参数,也不能完全避免发生颤振,最好的方法就是对其进行监测识别。
监测系统主要通过传感器来采集振动、声音等原始信号,对信号进行特征提取再利用算法判别状态,其框架如图2所示。
监测系统对于采集信号的传感器带宽、安放位置也有着严格的要求。传感器带宽要能准确覆盖颤振频率。安放位置原则上是必须离振源足够近才能采集到优质的信号。
2. 特征参数预处理
2.1 相关分析
原始信号的预处理是信号分析的前提[10]。功率、振动和AE(acoustic emission)等传感器在采集中被广泛应用,但各类传感器有利有弊:功率传感器灵敏度较低反应不够迅速;振动传感器信号强度易受外界影响;AE传感器更是会受到周围噪声干扰。所以,采用单一的传感信号进行监测难免会有弊端,试验使用的是多种传感器监测相结合,能够很好地弥补监测信号单一的缺点。
2.2 时域特征参数
对原始数据进行时域分析时,首先对信号波形、幅值和周期性进行初步判断,其次利用公式进行分析,常见的参数有极差、方差、标准差等。表1是有关时域特征参数的计算公式。
2.3 小波包分解
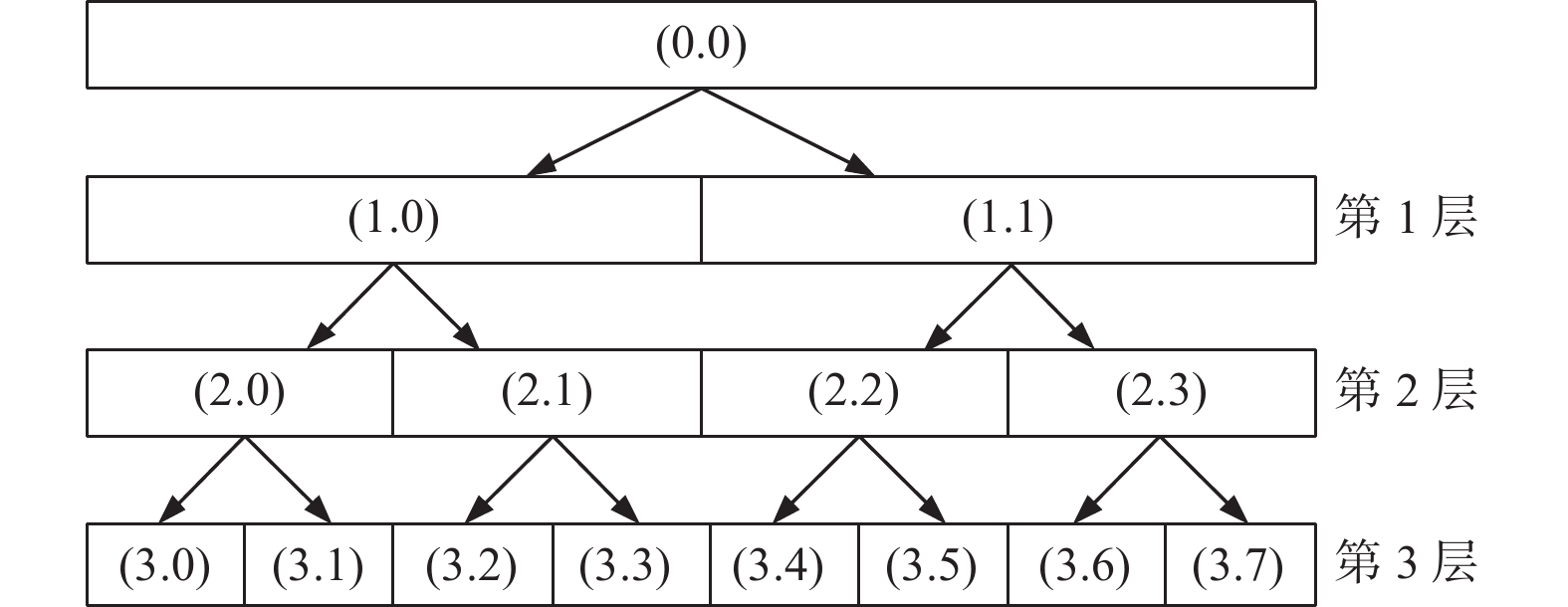
原始信号通过分解得到低频和高频分量,高频分量中含有大量的信号细节可以通过小波包提取。通常对原始信号进行3层小波包变换[11],信号被分配到8个节点中,其分解结构如图3所示。
表 1 时域特征参数计算公式Table 1. Calculation formula of time domain characteristic parameter参数 计算公式 参数 计算公式 标准差 $\sigma {\text{ = }}\sqrt {\dfrac{1}{n}\displaystyle\sum\limits_{i = 1}^n {{{({x_i} - \bar x)}^2}} } $ 方差 ${\sigma^2} = \dfrac{1}{{n - 1}}\displaystyle\sum\limits_{i = 1}^n {{{({x_i} - \bar x)}^2}} $ 极差 $R = {x_{\max }} - {x_{\min }}$ 均方根 ${X_{RMS}} = \sqrt {\left(\dfrac{1}{n}\displaystyle\sum\limits_{i = 1}^n {x_i^2} \right)} $ 均值 $\bar x = \dfrac{1}{n}\displaystyle\sum\limits_{i = 1}^n {{x_i}} $ 偏态系数 $C_{\rm s} = \dfrac{{\dfrac{1}{n}\displaystyle\sum\limits_{i = 1}^n {{{({x_i} - \bar x)}^3}} }}{{{{\left(\dfrac{1}{n}\displaystyle\sum\limits_{i = 1}^n {{{({x_i} - \bar x)}^2}} \right)}^{\textstyle\frac{3}{2}}}}}$ 峰值 ${X_{\text{p}}} = \max \left| {x(n)} \right|$ 峰值
因子$C = \dfrac{{{X_P}}}{{\sqrt {\left(\dfrac{1}{n}\displaystyle\sum\limits_{i = 1}^n {x_i^2} \right)} }}$ 若原始信号被分解到第
$j$ 层($j$ = 1, 2, 3···n),采样率为$f$ ,频带总数为$ {2^j} $ 个,第$ i $ 个频带范围为$\dfrac{f}{{{2^{j + 1}}}}i \sim $ $ \dfrac{f}{{{2^{j + 1}}}}\left( {i + 1} \right)$ 。分解层数越多,信号处理越精细。每个节点系数中存储的能量称为小波包节点能量,表达式为:
$$ E_j^i = \int_{ - \infty }^\infty {f_j^i{{\left( t \right)}^2}{\rm{d}}t} $$ (1) 其中:
$f_j^i\left( t \right)$ 和$E_j^i$ 分别是第$j$ 层第$i$ 个节点的小波系数和该系数的能量值。各系数能量值与总能量的比值为$$ {P_i} = E_j^i\Bigg/\sum_{j = 1}^n {E_j^i} $$ (2) 当颤振发生时,某个节点的能量值会骤增,因此能量占比很适合作为输入型特征参数用到一些算法模型中。
3. BP神经网络结构
3.1 基本原理
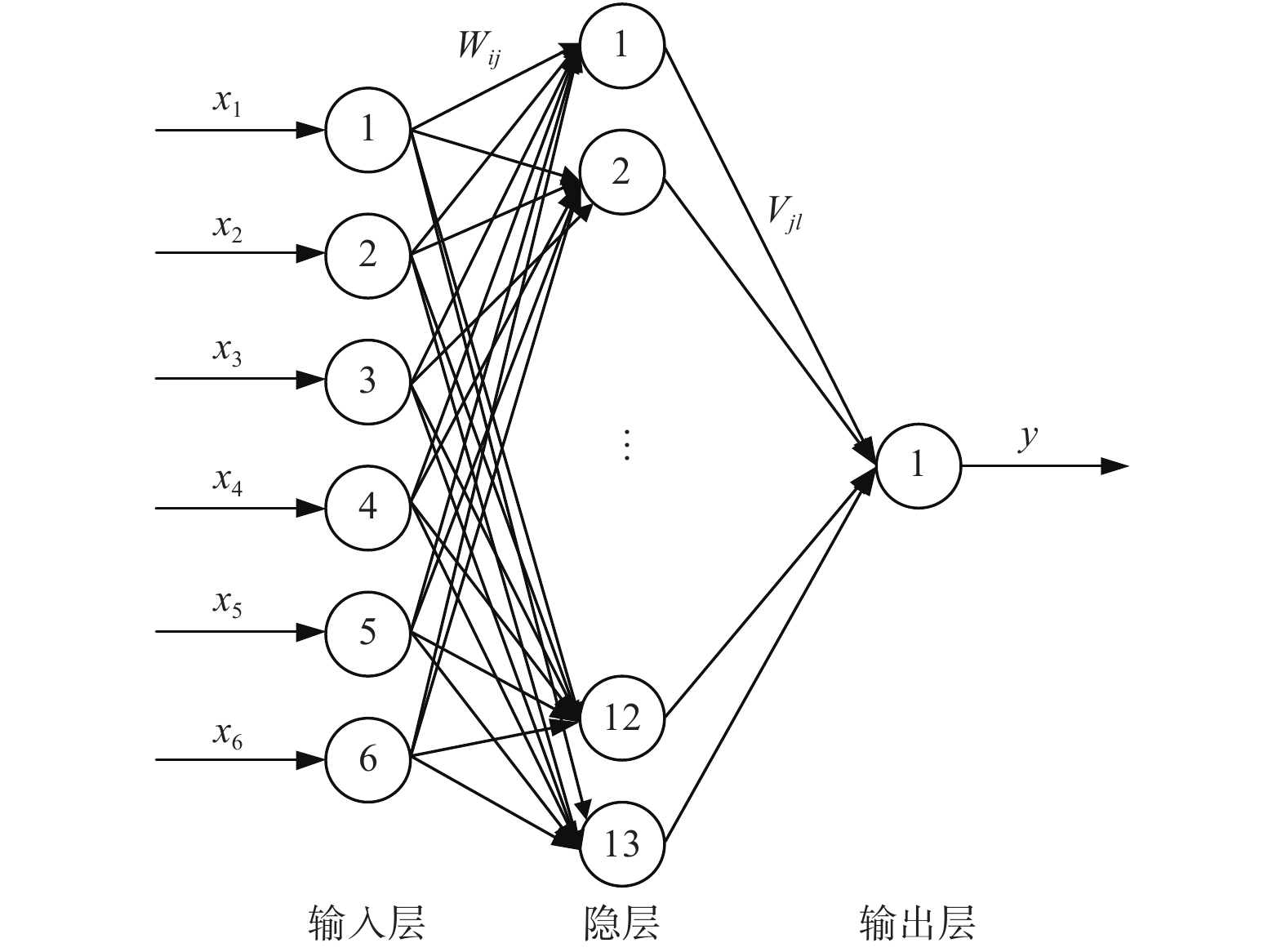
采用3层BP神经网络[12]对外圆磨床颤振在线识别。选择三向振动、AE传感器信号作为原始信号,BP神经网络输入层神经元数目设为
$n$ 个$\left( {n = 6} \right)$ 。根据Kolmogorov定理,综合考虑泛化学习能力,确定隐含层神经元数目k(k = 2n + 1,k = 13)。BP神经网络结构如图4所示。BP神经网络算法学习规则如下:表现函数沿着下降最快梯度方向,并不断修正权值阈值:
$$ {x_{k + 1}} = {x_k} - {a_k}{g_k} $$ (3) 其中:
${g_k}$ 为表现函数的梯度;${a_k}$ 为学习速率;${x_k}$ 为权值阈值。在BP神经网络中,输入节点为${x_n}$ ,隐层节点的输出为${Z_k}$ ,输出节点为${y_m}$ 试验中的输入节点数共6个,隐层节点数13个,输出节点数1个。其中输入层与隐层间的网络权值为
${w_{ij}}$ ($i$ = 1, 2···n,$j$ = 1, 2···k),阈值为${\theta _j}$ ;隐层节点与输出节点之间的网络权值为${v_{jl}}$ ,阈值为${\theta _l}$ ($l$ = 1, 2···m, m为输出节点的数量)设定好期望后模型的计算公式如下:隐层节点的输出
$$ {Z_j} = f\left( {\sum_{j = 1}^n {{w_{ij}}{x_i} - {\theta _j}} } \right) $$ (4) 输出节点的输出
$$ {y_l} = f\left( {\sum_{j = 1}^k {{v_{jl}}{z_j} - {\theta _l}} } \right) $$ (5) 输出节点的误差
$$\begin{split} E &=\frac{1}{2} \sum_{l=1}^{m}\left(t_{1}-y_{l}\right)^{2}=\frac{1}{2} \sum_{l=1}^{m}\left(t_{1}-f\left(\sum_{j=1}^{k} v_{j l} z_{j}-\theta_{l}\right)\right)^{2} \\ & =\frac{1}{2} \sum_{l=1}^{m}\left\{t_{1}-f\left[\sum_{j=1}^{k} v_{j l} f \times \sum_{i=1}^{n}\left(w_{i j} x_{i}-\theta_{j}\right)-\theta_{l}\right]\right\}^{2} \end{split}$$ (6) 3.2 训练过程
在BP神经网络迭代算法中选择的是泛化精确度高的Levenberg-Marquardt函数,隐藏层选择的是双曲正切S型传递函数(tansig),输出层选择的是线性传输函数(purelin),训练函数和自适应学习函数分别是默认的trainlm和learngdm函数。
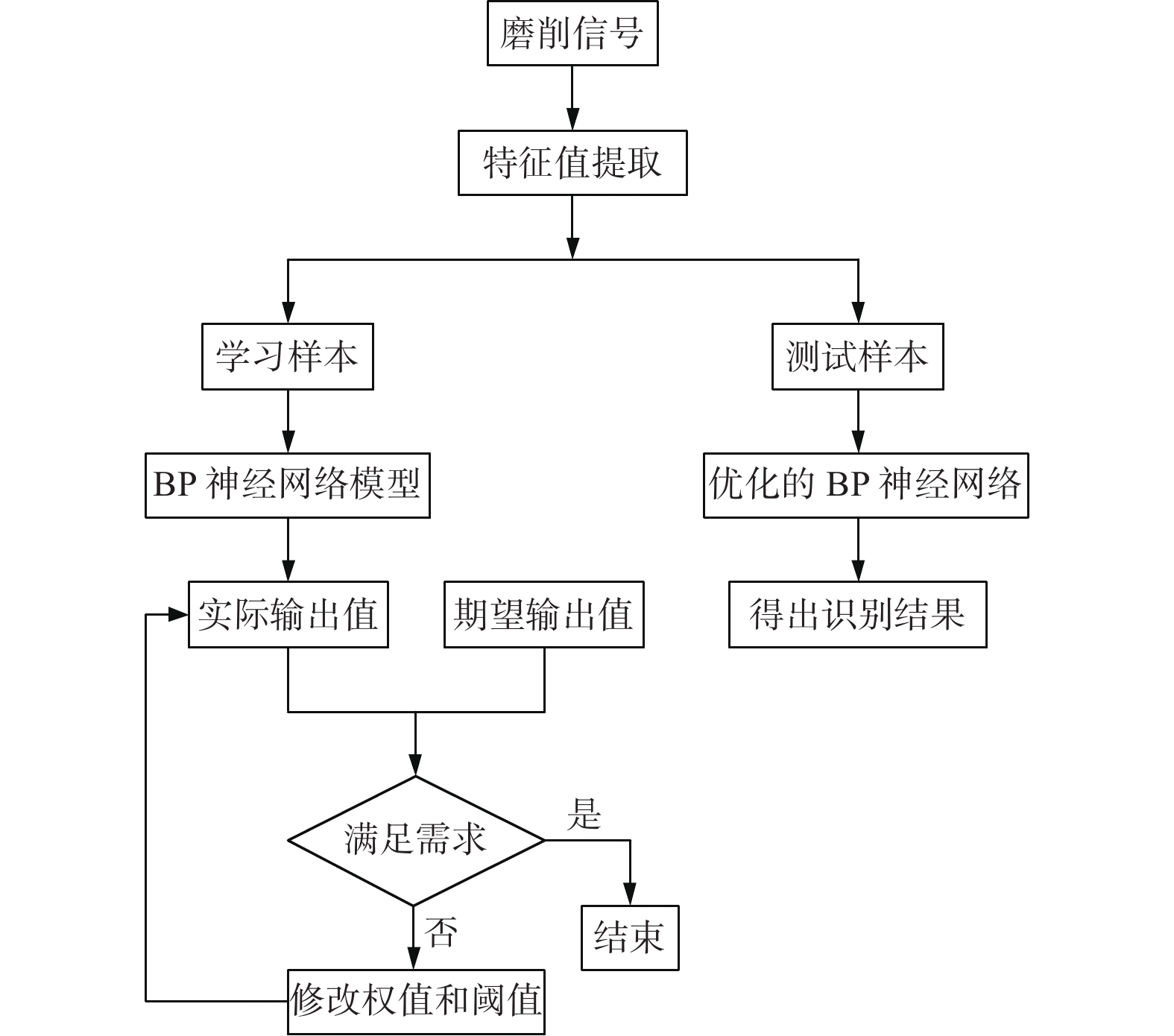
BP神经网络的自适应学习能力很强。通过发射传感器信号,对振动传感器信号进行特征处理并建立样本库。设定迭代精度和目标期望,利用迭代函数开始训练学习,不断地输出结果。如果输出结果与期望值相比超出设置精度,则反向传播。通过输出层不断逼近期望值,得到最优的BP神经网络模型,其过程如图5所示。
4. 试验设计和信号特征值提取
4.1 试验设计
利用高频AE、三向振动传感器进行信号采集,外圆磨床型号为M1432BX1500;砂轮直径为400 mm,磨削速度为35 m/s,磨削方式为外圆磨削,修整方式为金刚石笔修整(修整比为0.7),加工工件为普通轴承,工件材料为标准轴承钢。利用传感器底座的强磁特性,将AE传感器吸附在尾架顶尖上,三向振动传感器吸附在机床尾架上,试验现场图如图6所示。
传感器信号经过处理后输出到采集卡,并显示到PC端通过采集软件进行下步分析,总的测试流程如图7所示。
当磨削过程有颤振时,信号会发生变化,信号的时域、频域都能提供相应的信息。在试验中利用了AE传感器采集,所以可以通过小波包分解求出各频段的能量占比作为特征参数。
4.2 传感器信号采集及分解
砂轮转速和工件轴转速分别为53 m/s和110 r/min,保持不变,控制机床电机处于低速和高速2种状态。对AE传感器采集的原始信号进行小波包分解。采用db4小波分解得到与频段相对应的8个节点,频段间隔为62.5 kHz,频段为0~500 kHz。低速与高速下高频AE信号的各频段能量占比图分别如图8、图9所示:
将机床电机低速与高速2种状态下人小波包能量占比数据汇于表2中。由表2可知:低速和高速2种状态对比下,前3个节点处能量占比变化显著,后续节点中变化不明显,可以推出颤振发生频率集中在前3个节点处的信号频率部分。
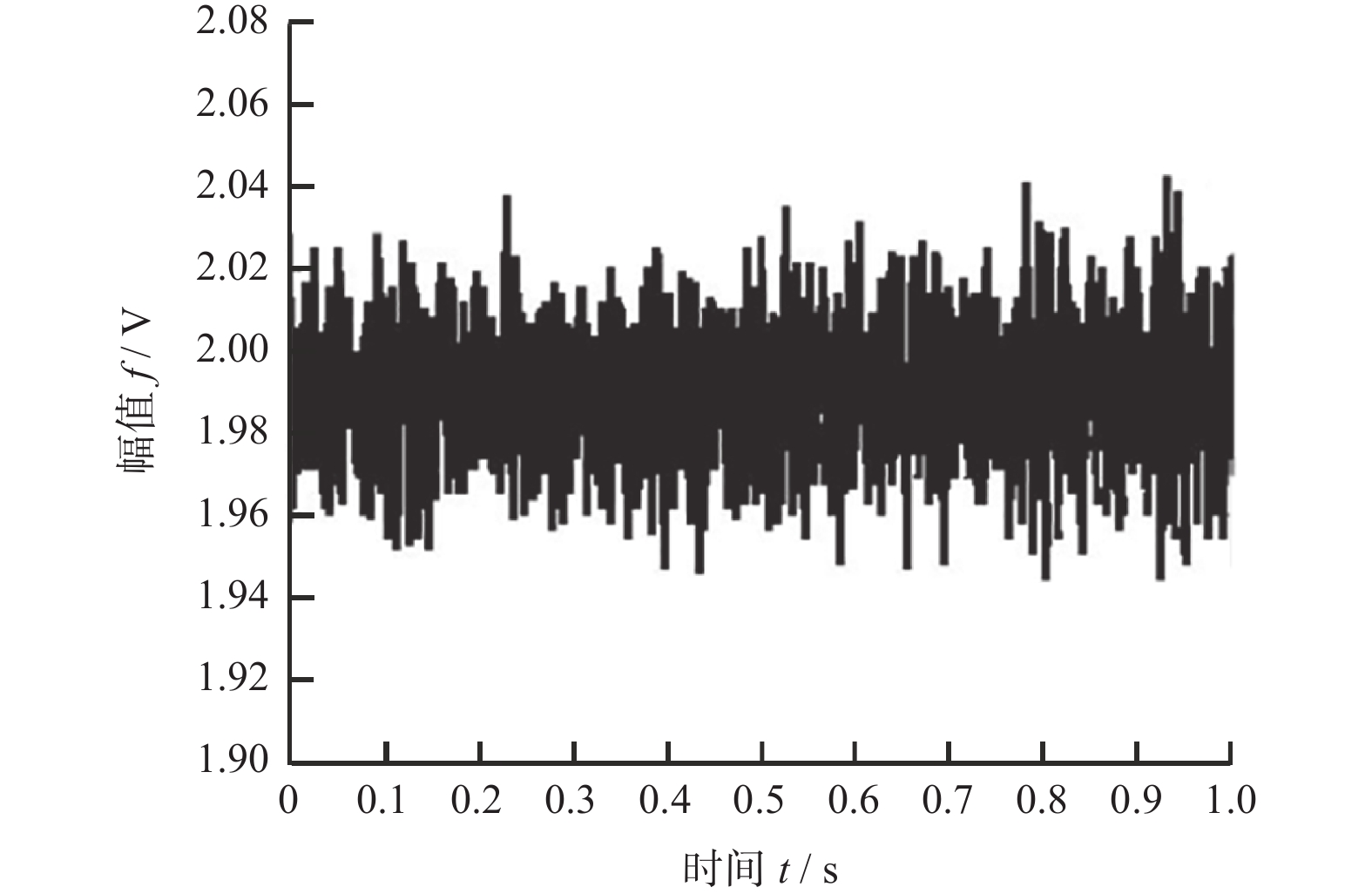
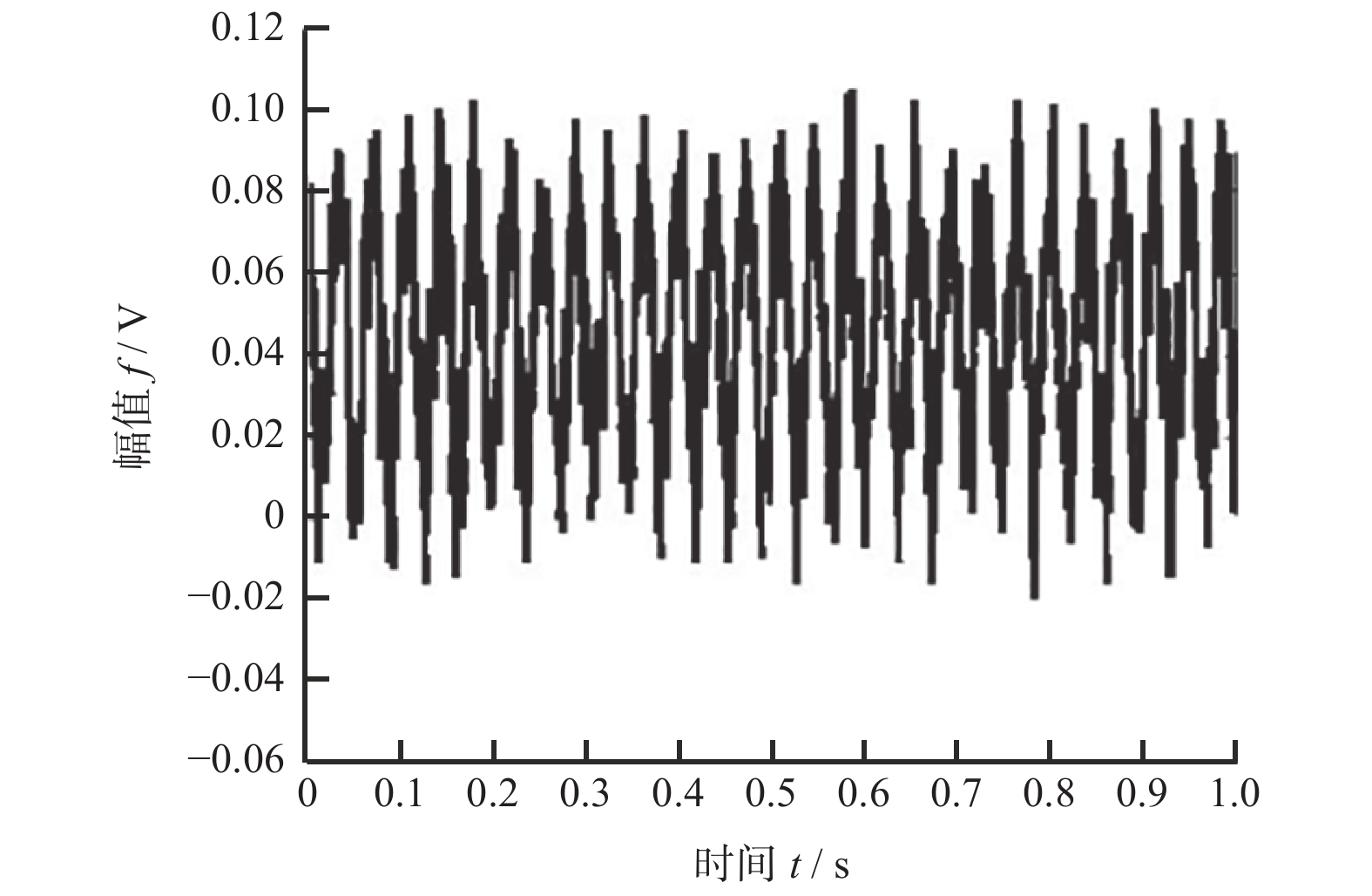
机床尾架处的振动时域信号由三向振动传感器采集,图10、图11、图12分别是x方向振动时域信号图、y方向振动时域信号图和z方向振动时域信号图,x方向的振动幅值主要在−0.04~0.06 V范围内变化,y方向振动幅值主要在1.92~2.04 V范围内变化,z方向振动幅值主要在−0.02~0.10 V范围内变化。可以看出在机床尾架处,与尾架x方向振动和尾架z方向振动相比,尾架y方向振动幅值变化更大,更易诱发磨削颤振现象的发生。
表 2 工件磨削AE频谱能量分布占比Table 2. AE spectrum energy distribution occupation of workpiece grinding节点 低速时能量占比 η1 / % 高速时能量占比 η2 / % 1 77.127 7 36.612 5 2 2.842 3 27.440 2 3 5.690 3 9.365 1 4 1.766 0 4.963 5 5 2.751 3 4.787 6 6 2.292 2 3.981 8 7 5.201 5 8.793 2 8 2.328 7 4.056 1 4.3 信号特征值提取
已知BP神经网络模型输出结果仅为有无颤振现象,将有无颤振现象赋值为{1,2}的集合对应监测的颤振结果。对传感器信号进行特征值提取,建立样本数据库。不同现象下的各信号值不同,主要是通过对声发射传感器采集到的原始信号进行小波包分解,并取与颤振现象发生频率接近的前3个节点处的能量占比作为声发射传感器的信号特征值,对振动传感器采集到的原始信号进行时域处理,选取x方向振动的均方根、y方向振动的偏态系数,z方向振动的标准差作为振动特征参数继而建立信号特征样本数据库。表3为高频采样下电机高速运转时声发射小波包能量占比数据。表4为高频采样下电机低速运转时的声发射小波包能量占比数据。表5为三向振动信号特征值数据,前80组是发生颤振时的振动特征值,后80组是无颤振时的振动特征值。通过对正常磨削和发生颤振现象时的信号特征值计算得到表3、表4、表5的样本数据库,利用样本数据库结合BP神经网络模型可以对颤振现象进行监测及识别。
表 3 高频声发射小波包能量占比(高速)Table 3. High frequency acoustic emission wavelet packet energy ratio (high speed)
序号能量占比 η3 / %
现象节点1 节点2 节点3 1 36.6 22.0 10.5 有颤振 2 34.3 21.9 11.1 有颤振 3 30.9 13.8 14.7 有颤振 ··· ··· ··· ··· ··· 78 36.1 21.9 10.3 有颤振 79 35.3 21.8 10.5 有颤振 80 29.7 14.3 14.3 有颤振 表 4 高频声发射小波包能量占比(低速)Table 4. High frequency acoustic emission wavelet packet energy ratio (high speed)
序号能量占比 η4 / %
现象节点1 节点2 节点3 1 78.5 1.78 5.33 无颤振 2 78.0 2.00 5.40 无颤振 3 78.5 1.81 5.30 无颤振 ··· ··· ··· ··· ··· 78 78.2 1.57 5.47 无颤振 79 78.0 1.65 5.55 无颤振 80 77.7 1.87 5.56 无颤振 表 5 三向振动信号特征值提取Table 5. Eigenvalue extraction of three-way vibration signal序号 x轴振动信号
均方根XRMSy轴振动信号
偏态系数$Cs$z轴振动信号
标准差$\sigma $现象 1 0.022 8 0.005 6 0.021 6 有颤振 2 0.021 4 0.030 5 0.017 3 有颤振 3 0.019 6 −0.082 7 0.014 9 有颤振 ··· ··· ··· ··· ··· 158 0.141 8 0.035 9 0.012 1 无颤振 159 0.141 7 0.087 0 0.011 7 无颤振 160 0.141 8 −0.011 0 0.011 8 无颤振 5. 网络训练及识别结果
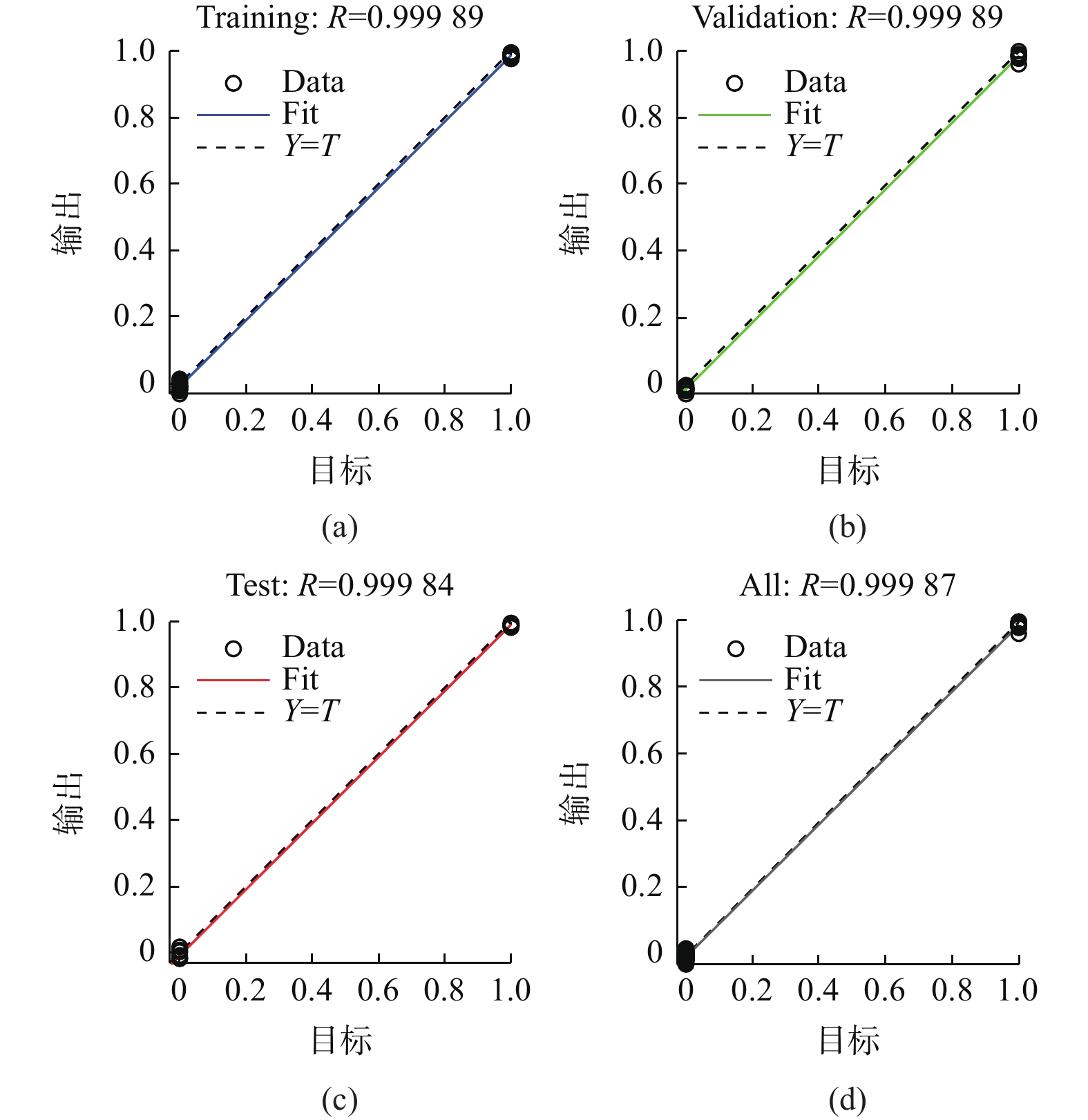
通过BP神经网络[13-14]算法将表5的160组信号特征值样本随机排列后分为150组训练样本和10组预测样本。模型输入为6个特征向量,输出为1个结果向量,如图13所示。BP神经网络训练时,训练次数设为1 000次,误差精度为
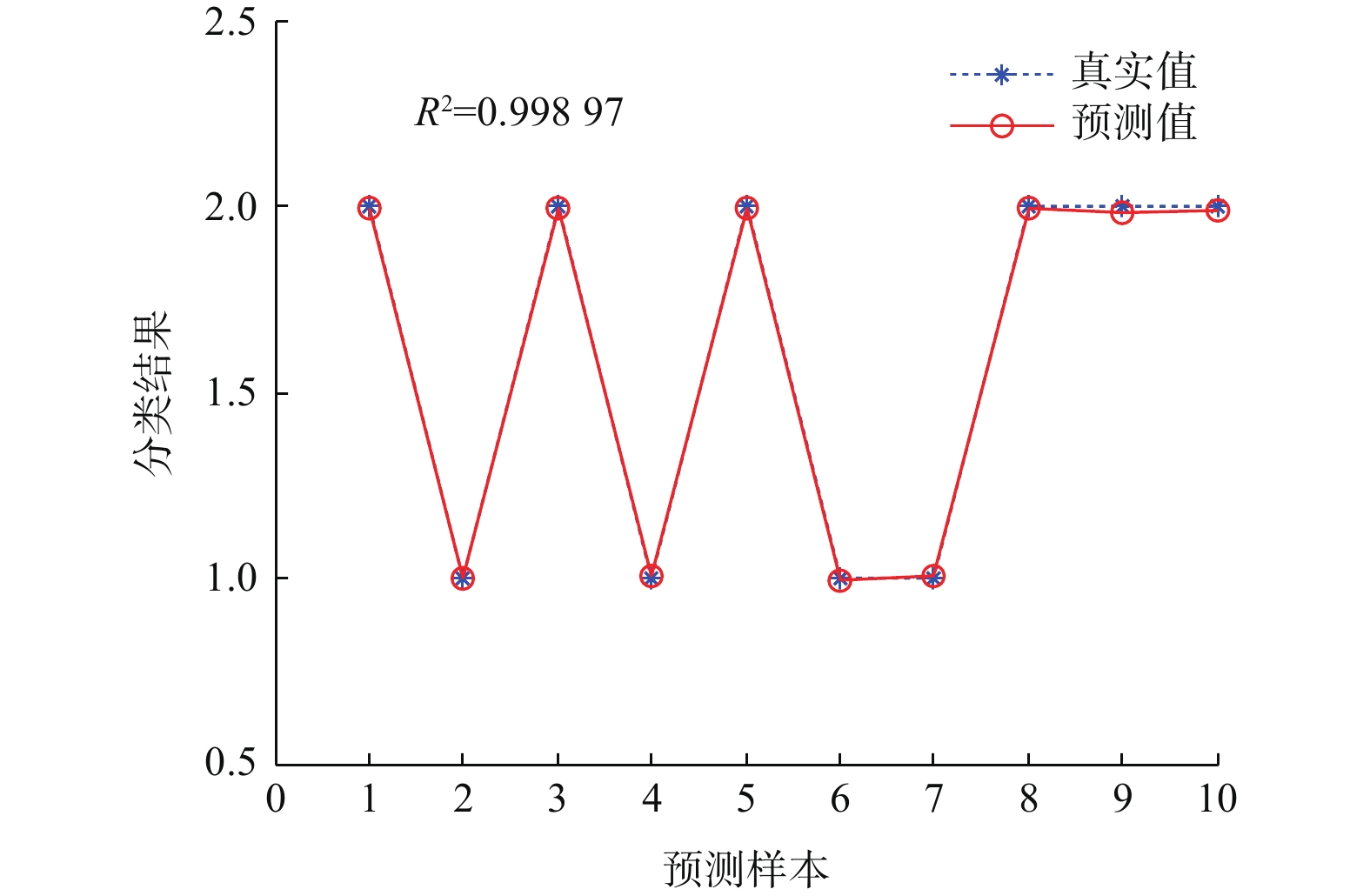
$ {10}^{-3} $ ,结果中的$ {R}^{2} $ 越接近于1,模型效果越好[9-10]。训练和识别过程以及10组预测样本得到的外圆磨削颤振真实值和预测值对比结果如图14所示:BP神经网络训练过程中的$ {R}^{2} $ 值大小约为0.99,说明BP神经网络模型训练过程较好。从图15中的BP神经网络颤振识别结果看出,真实值和预测样本的颤振预测结果均一致。表6为磨削颤振试验值与预测结果对比表。从表6可以看出:BP神经网络模型可以对外圆磨削颤振现象有效的在线监测和识别,同时算法平均误差在0.49%,预测结果均正确。
表 6 预测结果数据Table 6. Forecast result data序号 真实值 预测值 算法误差 现象 预测结果 1 2.000 0 1.991 5 0.42% 无颤振 正确 2 1.000 0 1.001 2 0.12% 有颤振 正确 3 2.000 0 1.992 8 0.36% 无颤振 正确 4 1.000 0 1.008 0 0.80% 有颤振 正确 5 2.000 0 1.992 3 0.39% 无颤振 正确 6 1.000 0 0.994 6 0.54% 有颤振 正确 7 1.000 0 1.005 4 0.54% 有颤振 正确 8 2.000 0 1.992 6 0.37% 无颤振 正确 9 2.000 0 1.982 9 0.85% 无颤振 正确 10 2.000 0 1.990 5 0.47% 无颤振 正确 6. 结论
针对外圆磨削颤振现象,使得工件加工表面质量降低,提出基于多特征参数样本和BP神经网络的外圆磨削颤振智能监测及识别方法,并通过试验进行算法验证,得到如下结论:
(1)时域特征参数结合小波包分解建立的多特征参数样本库能有效表征机床正常磨削和磨削颤振信息,同时也能保证BP神经网络监测模型分类精度。
(2)利用多特征参数样本库对BP神经网络训练学习,通过试验验证,BP神经网络算法模型能有效识别外圆磨削颤振现象,算法平均误差0.49%。
-
表 1 时域特征参数计算公式
Table 1. Calculation formula of time domain characteristic parameter
参数 计算公式 参数 计算公式 标准差 $\sigma {\text{ = }}\sqrt {\dfrac{1}{n}\displaystyle\sum\limits_{i = 1}^n {{{({x_i} - \bar x)}^2}} } $ 方差 ${\sigma^2} = \dfrac{1}{{n - 1}}\displaystyle\sum\limits_{i = 1}^n {{{({x_i} - \bar x)}^2}} $ 极差 $R = {x_{\max }} - {x_{\min }}$ 均方根 ${X_{RMS}} = \sqrt {\left(\dfrac{1}{n}\displaystyle\sum\limits_{i = 1}^n {x_i^2} \right)} $ 均值 $\bar x = \dfrac{1}{n}\displaystyle\sum\limits_{i = 1}^n {{x_i}} $ 偏态系数 $C_{\rm s} = \dfrac{{\dfrac{1}{n}\displaystyle\sum\limits_{i = 1}^n {{{({x_i} - \bar x)}^3}} }}{{{{\left(\dfrac{1}{n}\displaystyle\sum\limits_{i = 1}^n {{{({x_i} - \bar x)}^2}} \right)}^{\textstyle\frac{3}{2}}}}}$ 峰值 ${X_{\text{p}}} = \max \left| {x(n)} \right|$ 峰值
因子$C = \dfrac{{{X_P}}}{{\sqrt {\left(\dfrac{1}{n}\displaystyle\sum\limits_{i = 1}^n {x_i^2} \right)} }}$ 表 2 工件磨削AE频谱能量分布占比
Table 2. AE spectrum energy distribution occupation of workpiece grinding
节点 低速时能量占比 η1 / % 高速时能量占比 η2 / % 1 77.127 7 36.612 5 2 2.842 3 27.440 2 3 5.690 3 9.365 1 4 1.766 0 4.963 5 5 2.751 3 4.787 6 6 2.292 2 3.981 8 7 5.201 5 8.793 2 8 2.328 7 4.056 1 表 3 高频声发射小波包能量占比(高速)
Table 3. High frequency acoustic emission wavelet packet energy ratio (high speed)
序号能量占比 η3 / %
现象节点1 节点2 节点3 1 36.6 22.0 10.5 有颤振 2 34.3 21.9 11.1 有颤振 3 30.9 13.8 14.7 有颤振 ··· ··· ··· ··· ··· 78 36.1 21.9 10.3 有颤振 79 35.3 21.8 10.5 有颤振 80 29.7 14.3 14.3 有颤振 表 4 高频声发射小波包能量占比(低速)
Table 4. High frequency acoustic emission wavelet packet energy ratio (high speed)
序号能量占比 η4 / %
现象节点1 节点2 节点3 1 78.5 1.78 5.33 无颤振 2 78.0 2.00 5.40 无颤振 3 78.5 1.81 5.30 无颤振 ··· ··· ··· ··· ··· 78 78.2 1.57 5.47 无颤振 79 78.0 1.65 5.55 无颤振 80 77.7 1.87 5.56 无颤振 表 5 三向振动信号特征值提取
Table 5. Eigenvalue extraction of three-way vibration signal
序号 x轴振动信号
均方根XRMSy轴振动信号
偏态系数$Cs$z轴振动信号
标准差$\sigma $现象 1 0.022 8 0.005 6 0.021 6 有颤振 2 0.021 4 0.030 5 0.017 3 有颤振 3 0.019 6 −0.082 7 0.014 9 有颤振 ··· ··· ··· ··· ··· 158 0.141 8 0.035 9 0.012 1 无颤振 159 0.141 7 0.087 0 0.011 7 无颤振 160 0.141 8 −0.011 0 0.011 8 无颤振 表 6 预测结果数据
Table 6. Forecast result data
序号 真实值 预测值 算法误差 现象 预测结果 1 2.000 0 1.991 5 0.42% 无颤振 正确 2 1.000 0 1.001 2 0.12% 有颤振 正确 3 2.000 0 1.992 8 0.36% 无颤振 正确 4 1.000 0 1.008 0 0.80% 有颤振 正确 5 2.000 0 1.992 3 0.39% 无颤振 正确 6 1.000 0 0.994 6 0.54% 有颤振 正确 7 1.000 0 1.005 4 0.54% 有颤振 正确 8 2.000 0 1.992 6 0.37% 无颤振 正确 9 2.000 0 1.982 9 0.85% 无颤振 正确 10 2.000 0 1.990 5 0.47% 无颤振 正确 -
[1] MUNOA J, BEUDAERT X, DOMBOVVARIZ, et al. Chatter suppression techniques in metal cutting [J]. CIRP Annals-Manufacturing Technology,2016,65(2):785-808. doi: 10.1016/j.cirp.2016.06.004 [2] 江卓达, 何永义. 磨削颤振特性研究进展 [J]. 制造技术与机床, 2012(9): 35-42.JIANG Zhuoda, HE YongYi. Advances of research on the character of grinding chatter [J]. Manufacturing Technology and Machine Tools, 2012(9): 35-42. [3] 于骏一, 周晓勤. 切削颤振的预报控制 [J]. 中国机械工程, 1999, 10(9): 1028-1032.YU Junyi, ZHOU Xiaoqin. Predictive control of cutting chatter [J]. China Mechanical Engineering, 1999, 10(9): 1028-1032. [4] 孔繁森, 于骏一, 勾治践. 颤振状态的模糊识别 [J]. 振动工程学报, 1998(3): 81-85.KONG Fansen, YU Junyi, GOU Zhijian. Fuzzy identification of flutter state [J]. Journal of Vibration Engineering, 1998(3): 81-85. [5] 钱士才, 孙宇昕, 熊振华. 基于支持向量机的颤振在线智能检测 [J]. 机械工程学报, 2015(20): 1-8.QIAN Shicai, SUN Yuxin, XIONG Zhenhua. Support vector machine based online intelligent chatter detection [J]. Journal of Mechanical Engineering, 2015(20): 1-8. [6] 吕长飞, 吴小玉, 王茵, 等. 外圆磨削颤振监测方法设计 [J]. 机床与液压, 2019, 47(8): 166-168, 66.LYU Changfei, WU Xiaoyu, WANG Yin, et al. Design of chatter detection in external cylindrical grinding [J]. Machine Tools and Hydraulics, 2019, 47(8): 166-168, 66. [7] KULJANIC E, TOTIS G, SORTINO M. Development of an intelligent multisensor chatter detection system in milling [J]. Mechanical Systems and Signal Processing,2009,23(5):1704-1718. doi: 10.1016/j.ymssp.2009.01.003 [8] 黄强, 张根保, 张新玉. 对再生型切削颤振模型的试验分析 [J]. 振动工程学报, 2008, 21(6): 547-552.HUANG Qiang, ZHANG Genbao, ZHANG Xinyu. Experimental analysis on regenerative chatter model [J]. Journal of Vibration Engineering, 2008, 21(6): 547-552. [9] 王海龙. 机床颤振分析及抑制方法研究 [D]. 哈尔滨: 哈尔滨工程大学, 2013.WANG Hailong. Research on chatter analysis and suppression method of machine tool [D]. Harbin: Harbin Engineering University, 2013. [10] 李泽阳, 郑飂默, 李备备, 等. 基于改进BP神经网络的机床温度预警 [J]. 组合机床与自动化加工技术, 2021(9): 81-84, 89.LI Zeyang, ZHENG Liaomo, LI Beibe, et al. Temperature warning of machine tool based on improved BP neural network [J]. Modular Machine Tool and Automatic Machining Technology, 22021(9): 81-84, 89. [11] 谢峰云, 曹青松, 黄志刚. 基于小波包-BP神经网络的切削颤振监测 [J]. 仪表仪器与传感器, 2015(10): 88-90.XIE Fengyun, CAO Qingsong, HUANG Zhigang. Chatter monitoring based on wavelet packet and BP neural network [J]. Instruments and Sensors, 2015(10): 88-90. [12] 张强, 刘志恒, 王海舰, 等. 基于BP神经网络的截齿磨损程度在线监测 [J]. 中国机械工程, 2017, 28(9): 1062-1068.ZHANG Qiang, LIU Zhiheng, WANG Haijian, et al. On-line monitoring of pick’s wear degrees based on BP neural network [J]. China Mechanical Engineering, 2017, 28(9): 1062-1068. [13] 侯智, 曾杰. 基于BP神经网络的轴承套圈沟道磨削粗糙度识别 [J]. 机械设计与研究, 2019, 35(3): 119-122.HOU Zhi, ZENG Jie. Roughness identification of bearing ring groove grinding based on bp neural network [J]. Mechanical Design and Research, 2019, 35(3): 119-122. [14] 谢锋云, 江炜文, 陈红年, 等. 基于广义BP神经网络的切削颤振识别研究 [J]. 振动与冲击, 2018, 37(5): 65-70, 78.XIE Fengyun, JIANG Weiwen, CHEN Hongnian, et al. Cutting chatter recognition based on generalized BP neural network [J]. Vibration and Shock, 2018, 37(5): 65-70, 78. 期刊类型引用(7)
1. 王树龙,田俊超,康仁科,董志刚,鲍岩. 薄壁CFRP管端面磨削稳定性实验研究. 金刚石与磨料磨具工程. 2025(02): 189-196 .  本站查看
本站查看2. 杨浩,谢晋,陈佳欣,陈钊杰,何铨鹏. 金刚石磨粒切削-滚压钛合金的干磨削系统控制. 机械工程学报. 2025(09): 168-177 .  百度学术
百度学术3. 刘伟,刘旺,曹大虎,葛吉民,万林林,陈加. 基于改进EMD和GA-BPNN的机器人磨削颤振监测. 振动与冲击. 2024(09): 131-138+174 .  百度学术
百度学术4. 王岩. 基于声发射监测的微磨削特征信号感知测量. 机械管理开发. 2024(09): 44-45+48 .  百度学术
百度学术5. 张海霞. 基于BP-GA算法的时栅传感器信号健康状况预测. 电子产品世界. 2023(06): 51-53 .  百度学术
百度学术6. 赵燕燕,汤瑞,习岗,俞生伟. 基于FTA优化CPSO算法的锻压机典型故障诊断研究. 机床与液压. 2023(24): 192-196 .  百度学术
百度学术7. 朱子俊,朱祥龙,董志刚,康仁科,鲍岩. 磨削加工颤振稳定性研究综述. 机械工程学报. 2023(21): 15-33 .  百度学术
百度学术其他类型引用(5)
-





 下载:
下载:

















































 下载:
下载:







 百度学术
百度学术















 邮件订阅
邮件订阅 RSS
RSS
