Energy consumption modeling and parameter optimization of tower combined diamond circular saw blade
-
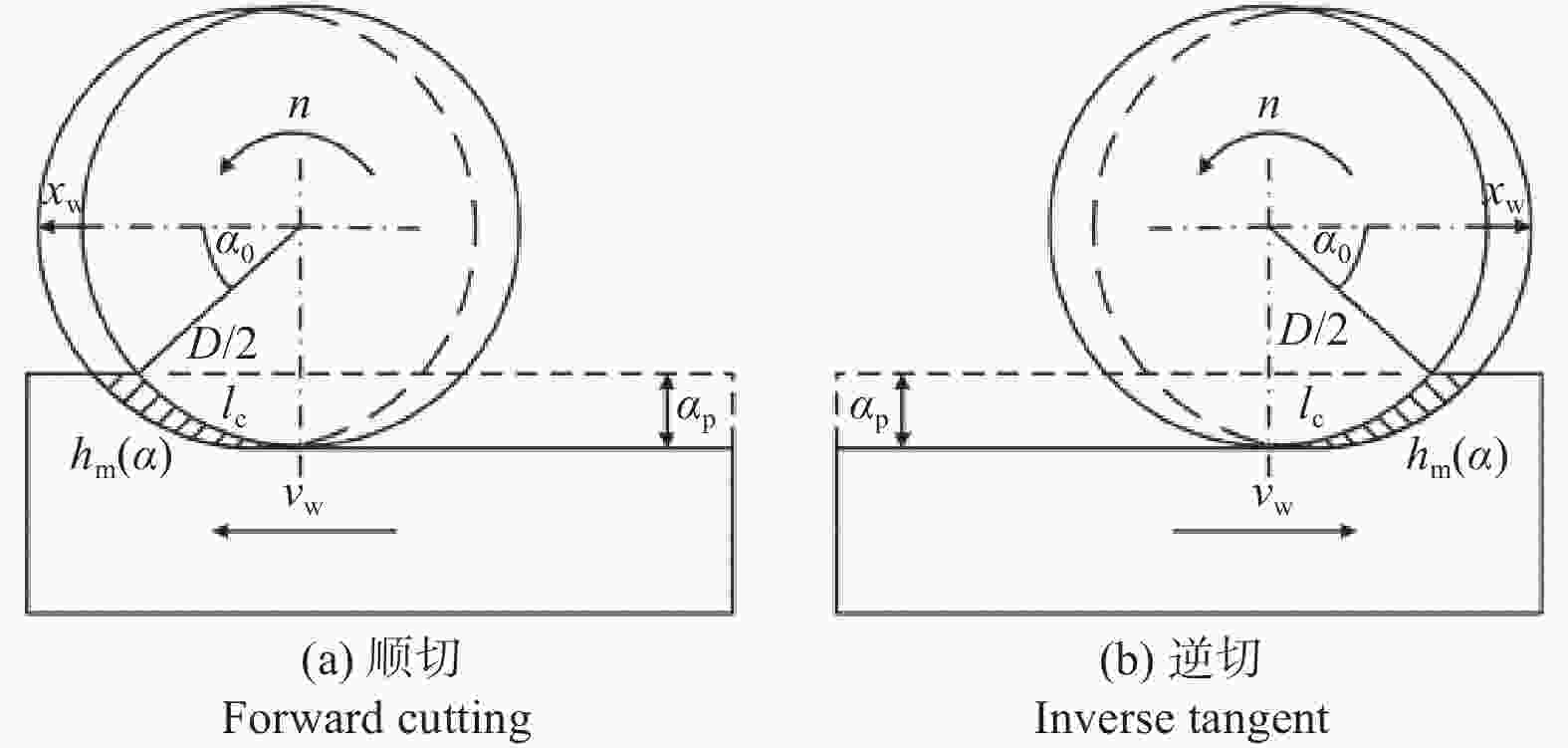
摘要: 为准确预测塔形组合式金刚石圆盘锯在荒料锯切过程中的功率，以组合锯切系统中单锯片的单磨粒平均未变形切屑厚度为媒介，建立了锯切功率的参数模型，并对其进行修正，提出一种少样本快速预测模型，通过锯切实验测量不同参数组合下的锯切功率，采用多元线性回归方法拟合数据以获取可靠的模型系数。最后以锯切参数为优化变量，以锯切比能和锯切时间最小为优化目标建立优化模型，并采用改进粒子群算法对模型进行优化求解。试验结果表明，参数模型充分解释了各锯切参数对锯切功率的影响，能够准确预测不同锯片组合方式下的锯切功率，改进的粒子群算法有较高的优化性能，使用优化后的参数能够显著降低锯切功率。
-
关键词:
- 塔形组合式金刚石圆盘锯 /
- 能耗模型 /
- 平均未变形切屑厚度 /
- 参数优化
Abstract: To precisely forecast the power of a tower combined diamond circular saw blade during material sawing, a model for sawing power was established using the average thickness of an undeformed chip from a single grinding grain of an individual saw blade within the combination saw as a medium. This model was then refined to enhance accuracy. A fast and accurate prediction model, requiring only a small number of samples, was developed. Sawing power was measured through various parameter combinations via sawing experiments, and model coefficients were obtained by fitting the data using multivariate linear regression techniques. An optimization model was subsequently established, with sawing parameters as optimization variables. The objectives of this model were to minimize sawing specific energy and reduce sawing time. An optimized particle swarm algorithm was adopted to solve the model. The experimental results reveal that the parameter model can comprehensively elucidate the influence of various sawing parameters on sawing power, with the model accurately forecasting the sawing power under different saw blade combinations. The improved particle swarm algorithm demonstrates strong optimization performance, with optimized parameters contributing to significant reductions in sawing power. -
荒料锯切是石材制品生产过程中第一道也是最重要的一道工序，塔形组合式圆盘锯（简称组合锯）由于优越的切割性能在荒料锯切中得到广泛应用。组合锯在使用阶段耗电量大、间接碳排放量高，对组合锯锯切过程进行能耗建模、评估与优化可以有效节约能源，减少加工过程对环境的污染，增加企业利润，对石材行业绿色健康可持续发展具有重要意义。
目前已有大量学者对圆盘锯的能耗预测和优化进行了深入研究。TURCHETTA等[1-2]以等效切屑厚度为基础分析了锯切功率和锯切参数的关系，指出锯切功率受锯切深度和进给速度影响显著；黄国钦等[3-4]以锯切接触弧区内单磨粒切削深度为桥梁建立了不同锯切速度下的锯切功率模型，能够实现同一线速度不同锯切参数下功率的预测。张昆等[5]采用反向传播（back propagation，BP）神经网络建立磨削能耗预测模型，并采用动态惯性权重改进粒子群算法，以能耗最小为优化目标对加工参数进行优化，使用优化后的参数能够显著降低磨削能耗；陈行政等[6]系统分析了多刀具孔加工过程的能耗，采用粒子群算法以最小化加工能耗和加工时间为优化目标，对刀具直径和加工参数进行优化求解，使用优化后的参数显著降低了加工能耗，缩短了加工时间。
综上所述，目前的能耗建模方法仅适用于单片锯，由于组合锯锯片之间复杂的相互作用，这些能耗模型并不适用于组合锯，亟需一种新的能耗建模方法来实现组合锯的能耗预测，且目前对于锯切参数的优化主要考虑的是加工过程的能耗，少有关于锯切比能（specific energy consumption，SEC）的研究，不利于提高能量利用率。基于此，本文以组合锯中单锯片的单磨粒平均未变形切屑厚度为媒介，建立了组合锯锯切功率的预测模型，通过锯切实验验证模型的准确性，并对模型进行修改，设计了一种少样本快速预测模型。在预测模型的基础上，以锯切参数为优化变量，以锯切比能和锯切时间最小为优化目标建立优化模型，提出一种基于改进粒子群算法的优化求解方法。
1. 锯切能耗模型
1.1 组合锯结构组成
组合锯是将多个圆锯片以一定的间隔组合安装在同一根主轴上，同时对石材荒料进行锯切的加工设备，如图1所示。
组合锯上的锯片按照直径由小到大安装在主轴上，符合等差数列，小锯片的径厚较小、稳定性好，因而锯切时先由小锯片开槽，在完成开槽后，锯机横向移动一个板材厚度，大锯片沿着小锯片形成的锯路锯切，实现总锯切深度逐渐增加的分层锯切。与传统切割方式相比，组合锯的切割过程更加稳定，切割质量更好，而且可显著降低成本，提高效率。
1.2 组合锯能耗模型
锯切过程中，组合锯通过金刚石颗粒在锯切弧区内去除小体积切屑实现材料的去除，能量主要消耗在材料的塑性变形、脆性断裂以及摩擦等方面，这些能量的消耗与单颗金刚石磨粒的平均未变形切屑厚度hm有直接关系[7]。在单颗磨粒进出锯切弧区的过程中，其未变形切屑厚度变化如图2所示。
图 2 单颗磨粒未变形切屑厚度变化示意图Figure 2. Schematic diagram of the variation in undeformed chip thickness of a single abrasive particle根据KONSTANTY[8]的研究，第i张锯片的平均未变形切屑厚度hmi可表示为：
$$ {h_{{\text{m}}i}}{\text{ = }}\frac{{\displaystyle\int_{{\alpha _{0\_i}}}^{\tfrac{{\text{π}}}{2}} {{x_{\text{w}}}\cos \alpha {\text{d}}\alpha } }}{{\displaystyle\int_{{\alpha _{0\_i}}}^{\tfrac{{\text{π}}}{2}} {{\text{d}}\alpha } }} = \sqrt {\frac{{{v_{\text{w}}}}}{n}\frac{{1000}}{{\lambda {\text{π }}C{D_i}r}}\sqrt {\frac{{{a_{\text{p}}}}}{{{D_i}}}} } $$ (1) 式中：xw为连续锯切过程中单颗磨粒进给量，mm；α0_i为第i张锯片最大切屑厚度对应的瞬时切角；vw为进给速度，m/min；n为主轴转速，r/min；C为单位面积内的活性磨粒数量；λ为锯片的节段比；r为切屑比系数，即平均切屑宽度与平均切屑厚度之比；ap为切削深度，mm；Di为第i张锯片的直径，mm。
由式（1）可以得出，当锯片属性不变时，单颗磨粒的平均未变形切屑厚度直接由主轴转速n、进给速度vw和锯切深度ap决定。
LI等[9]指出在恒定切削状态下，锯切力随切屑厚度的增加近似成指数增加，将锯片各执行顺切和逆切1次视为1次完整锯切，则第i张锯片1次锯切过程中锯切弧区内理想单颗粒平均切向力fti可表示为：
$$ {f_{{\mathrm{t}}i}} = {k_{{\mathrm{t}}i}}h_{{\mathrm{m}}i}^{{\text{2}}x} $$ (2) 式中：kti为切削力系数；x为分布系数的1/2，在石材锯切领域，其值在[0,1]的范围内。
假定在单位宽度单位接触弧长上磨粒受力均匀，则锯切接触弧区内的切削力可表示为：
$$ {F_{{\mathrm{t}}i}} = B{l_{{\mathrm{c}}j}}C{f_{{\mathrm{t}}j}} = {K_{{\mathrm{t}}i}}a_{\mathrm{p}}^{{1 \mathord{\left/ {\vphantom {1 2}} \right. } 2}}h_{{\mathrm{m}}i}^{2x} $$ (3) 式中：B为锯片厚度，Kti为切削力分布系数，lcj为锯切接触弧长。
在小切深锯切中，lcj=(apDi)1 / 2，在安装锯片后锯片直径便固定，因此可以将Di视为常数项计算。
单锯片在锯切区域消耗的锯切功率pti可用锯切切向力fti和锯片圆周速度vsi表示，表达式为：
$$ {P_{{\mathrm{t}}i}} = {F_{{\mathrm{t}}i}}{v_{{\mathrm{s}}i}} = {K_{{\mathrm{t}}i}}\frac{{{\text{π }}{D_i}}}{{1000}}na_{\mathrm{p}}^{{1 \mathord{\left/ {\vphantom {1 2}} \right. } 2}}h_{{\mathrm{m}}i}^{2x} = {k_i}na_{\mathrm{p}}^{{1 \mathord{\left/ {\vphantom {1 2}} \right. } 2}}h_{{\mathrm{m}}i}^{2x} $$ (4) 式中：ki为待定系数，其值取决于锯片属性。
假设组合锯的总功率为系统中参与锯切的各锯片功率之和，则理想状态下m片锯第j种组合锯切方式的总功率pj可以表示为：
$$ {p_j} = \sum {{p_{{\mathrm{t}}i}} = } na_{\mathrm{p}}^{{1 \mathord{\left/ {\vphantom {1 2}} \right. } 2}}\sum {{k_i}h_{{\mathrm{m}}i}^{2x}} $$ (5) 实际锯切过程中，不同直径的锯片之间存在耦合效应，对锯切过程产生一系列附加影响，如增加锯片与荒料之间的摩擦、与石材碎屑的冲击等，造成额外的功率损失，这使得单锯片功率叠加之和一般小于组合功率[10-11]。
如图3所示，在存在耦合效应的锯切过程中，组合锯的功率和锯切参数仍呈指数相关，根据现有的研究，在不存在耦合效应的锯切过程中，锯机功率和锯切指数呈指数相关，因此将其视作锯切参数的幂函数，引入组合系数kcj来平衡组合方式带来的影响，表达式为：
图 3 功率随锯切参数变化示意图Figure 3. Schematic diagram of power variation with sawing parameters$$ {k_{{\mathrm{cp}}j}} = {k_{{\mathrm{c}}j}}{n^{{a_j}}}v_{\mathrm{w}}^{{b_j}}a_{\mathrm{p}}^{{c_j}} $$ (6) 则式（5）可转换为：
$$ {P_j} = {k_{{\mathrm{cp}}j}}\sum {{p_{{\mathrm{t}}i}}} = {k_{{\mathrm{c}}j}}{n^{1 + {a_j}}}v_{\mathrm{w}}^{{b_j}}a_{\mathrm{p}}^{{1 \mathord{\left/ {\vphantom {1 {2 + }}} \right. } {2 + }}{c_j}}\sum {{k_i}h_{{\mathrm{m}}i}^{2x}} $$ (7) 式中：kcpj为耦合系数；kcj为耦合修正系数；aj、bj和cj为待定系数，受锯片属性与锯片组合方式的直接影响。
图4呈现了锯切功率和hm之间的关系。由于hm和锯切参数直接相关，因此以hm为媒介，在锯切弧区内平均切向力的基础上建立锯切功率Pj和锯切参数的关系：
$$ \begin{split} {P_j} =\, &{k_{{\mathrm{c}}j}}{n^{1 + {a_j}}}v_{\mathrm{w}}^{{b_j}}a_{\mathrm{p}}^{{1 \mathord{\left/ {\vphantom {1 {2 + }}} \right. } {2 + }}{c_j}}\sum {{k_i}} {\left( {\frac{{{v_{\mathrm{w}}}}}{n}\frac{{1000}}{{\lambda {\text{π }}C{D_i}r}}\sqrt {\frac{{{a_{\mathrm{p}}}}}{{{D_i}}}} } \right)^x} \\ {\text{ }} =\, & {K_j}{n^{1 - x + {a_j}}}v_{\mathrm{w}}^{x + {b_j}}a_{\mathrm{p}}^{1 + {{x + 2{c_j}} \mathord{\left/ {\vphantom {{x + 2{c_j}} 2}} \right. } 2}} \\ \end{split} $$ (8) 式中：Kj反映了锯片属性及锯片组合方式等对功率的影响。
本节中的理论模型系数由于涉及许多难以获取的设计和测试参数，可结合实验与统计分析方法通过回归拟合得到。
2. 模型验证、修改与分析
2.1 模型验证
为验证模型的准确性，需要进行锯切实验。实验选用MAX-3500-4D桥式切石机（超重型）为加工工具，安装锯片数量为4，锯片厚度均为7.2 mm，直径D1～D4分别为650 、1 050 、1 450 和1 850 mm。使用CW500电能质量分析仪对功率进行测试，针对组合锯的三相电路，采用三相三线（3P3W）接线方式，接线方式如图5所示。
综合考虑加工设备、荒料性质、操作工人经验以及企业推荐值等，确定如表1所示的锯切参数组合，每种锯切参数组合进行3次锯切实验。采集每种锯切参数组合下锯机的空转功率Pidle和稳定锯切功率Pin，通过公式P = Pin − Pidle获取锯切过程实际消耗的功率。
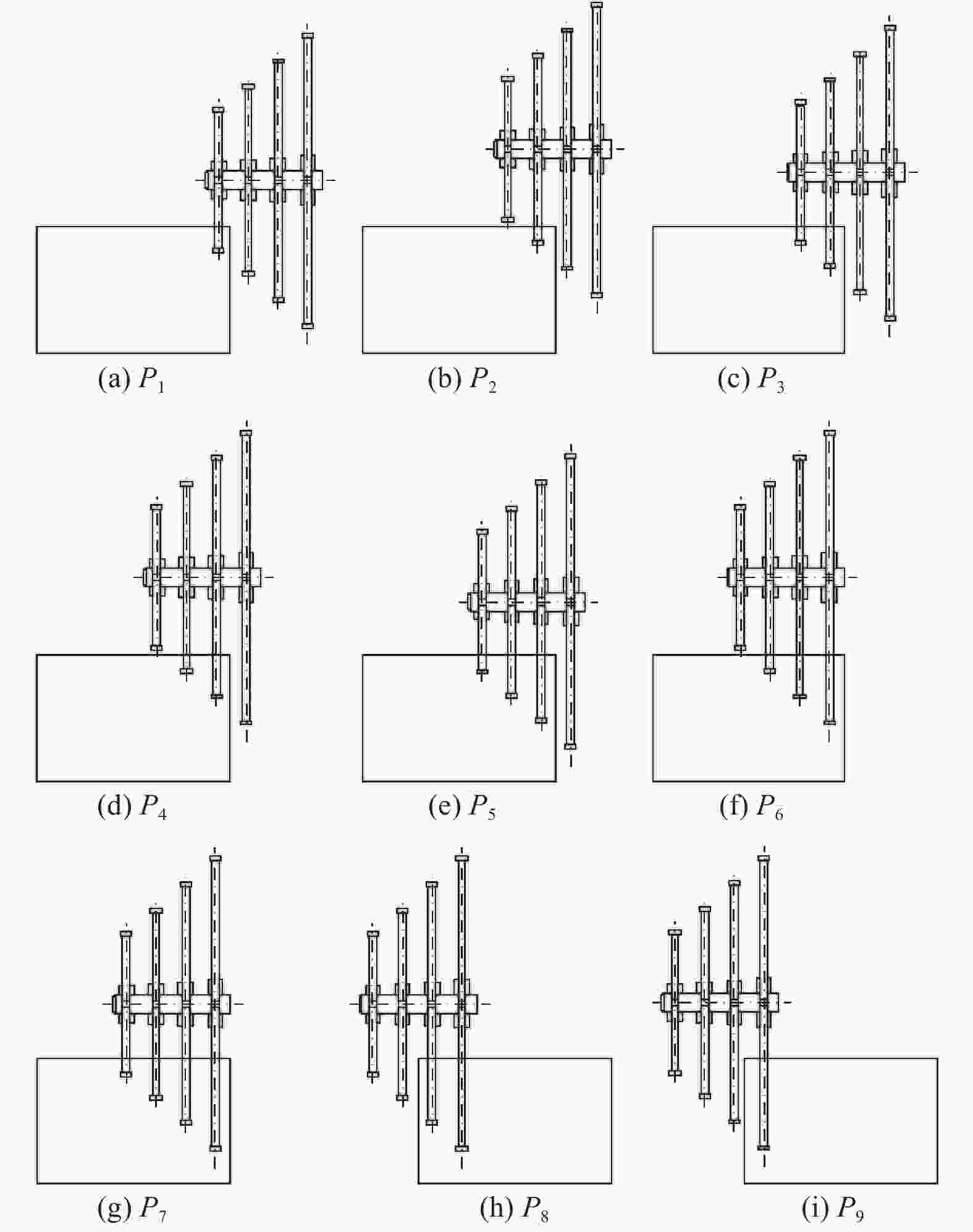
表 1 锯切参数组合Table 1. Sawing parameter combination参数 取值 转速 n / (r·min−1) 380，395，410 进给速度 vw / (m·min−1) 3.45，4.45，5.45 锯切深度 ap / mm 4，6，8 如图6所示，4片不同直径的锯片组合方式共有9种，其中后3片组合锯切功率P6和4片组合锯切功率P7最大，且在4片锯中这2种锯片组合锯切方式最为常用，因此对这2种组合锯切过程中的功率进行测量，测量结果列于表2。
表 2 锯切能耗测量结果Table 2. Measurement results of sawing energy consumption编号 转速 n /
(r·min−1)进给速度
vw / (m·min−1)锯切
深度
ap / mm后3片组合
锯切功率
P6 / kW4片组合
锯切功率
P7 / kW1 380 3.45 4 12.74 15.20 2 380 4.45 4 15.66 17.33 3 380 5.45 4 18.89 21.56 4 380 3.45 6 16.22 19.11 5 380 4.45 6 19.50 22.92 6 380 5.45 6 22.59 27.04 7 380 3.45 8 19.72 22.74 8 380 4.45 8 22.97 26.97 9 380 5.45 8 26.81 31.96 10 395 3.45 4 13.29 15.57 11 395 4.45 4 15.74 18.84 12 395 5.45 4 18.90 22.87 13 395 3.45 6 16.93 19.58 14 395 4.45 6 19.69 23.32 15 395 5.45 6 23.44 27.52 16 395 3.45 8 19.59 22.80 17 395 4.45 8 23.31 27.73 18 395 5.45 8 27.84 32.62 19 410 3.45 4 13.51 16.58 20 410 4.45 4 15.96 19.29 21 410 5.45 4 18.91 22.42 22 410 3.45 6 16.84 19.79 23 410 4.45 6 19.78 23.99 24 410 5.45 6 23.47 27.94 25 410 3.45 8 19.83 23.32 26 410 4.45 8 23.59 28.35 27 410 5.45 8 28.38 35.44 使用表2中的数据对非标准化模型系数Beta1进行求解，将求解的系数带入参数模型以实现对功率的预测。除了模型系数外，还要对标准化系数Beta2、方差膨胀因子VIF、德宾-沃森DW以及显著性Sig进行求解，其中Beta用于评价各锯切参数对功率的影响力大小，VIF用于评价各参数之间的共线性，DW用于评价各参数的自相关性。所得结果列于表3和表4。
表 3 P6模型拟合系数Table 3. Fitting coefficients of the P6 model系数 Beta1 Beta2 Sig VIF kcp6 0.144 <0.001 K6 0.248 0.033 x 0.543 <0.001 1.000 a 0.078 0.055 <0.001 1.000 b 0.204 0.655 <0.001 1.000 c −0.210 0.750 <0.001 1.000 R2 99.4% <0.001 DW 2.355 RMSE 0.017 表 4 P7模型拟合系数Table 4. Fitting coefficients of the P7 model系数 Beta1 Beta2 Sig VIF kcp7 0.171 <0.001 K7 0.027 <0.001 x 0.543 <0.001 1.000 a −0.312 0.109 <0.001 1.000 b 0.228 0.660 <0.001 1.000 c −0.205 0.737 <0.001 1.000 R2 99.0% <0.001 DW 1.808 RMSE 0.022 根据表3和表4可知，P6和P7参数模型的DW均值为2.000左右，各系数的VIF值均<5.000，表明各参数之间的自相关性以及共线性都很弱，参数之间相互独立；各锯切参数的显著性Sig均<0.050，表明锯切参数对锯切功率具有较好的解释作用，且模型回归显著性<0.050，因此可以认为参数模型具有较高的可靠性。P6和P7参数模型的决定系数分别为99.0%和99.4%，证明本文对耦合效应的选取是正确的，且模型对功耗的预测较为准确。
根据标准化系数Beta2可以得出，锯切深度ap、进给速度vw和主轴转速n对功率的影响逐渐减小。
为进一步验证模型的准确性，选取另外3组不同的锯切参数，在相同的锯切条件下进行荒料锯切实验，用上述模型进行功率预测，并与实测功率进行对比，所得结果列于表5和表6。
表 5 P6模型对比分析Table 5. Comparative analysis of the P6 model编号 转速 n
/ (r·min−1)进给速度vw /
(m·min−1)锯切深度ap / mm P预测 / kW P实测 / kW η / % 1 370 3.45 8 18.97 18.40 3.10 2 385 4.45 6 19.80 20.97 5.58 3 400 5.45 4 18.61 19.29 3.53 表 6 P7模型对比分析Table 6. Comparative analysis of the P7 model编号 转速 n
/ (r·min−1)进给速度vw /
(m·min−1)锯切深度ap / mm P预测 / kW P实测 / kW η / % 1 370 3.45 8 21.53 23.25 7.40 2 385 4.45 6 22.94 24.03 4.54 3 400 5.45 4 21.95 22.95 4.35 从以上3种方案的对比结果可以得出，模型的预测误差均在10.00%以内，能够很好地反映锯切参数和功率之间的关系，进一步验证了模型的可靠性。
2.2 模型修改和验证
由式（8）的模型可知，要实现组合锯各锯切方式下功率的预测，需要大量的实验数据作为支撑。因此对参数模型进行修改，以切割次数最多的锯片组合方式为基准，将该组合方式下耦合效应带来的影响视为锯切参数的函数，将其他组合锯切方式中耦合效应带来的影响视为该锯片组合的koj倍，则可将式（6）和式（8）修改为：
$$ {k_{{\mathrm{cp}}j}} = {k_{{\mathrm{o}}j}}{k_{\mathrm{c}}}{n^a}v_{\mathrm{w}}^ba_{\mathrm{p}}^c $$ (9) $$ {P_j} = {K_j}{n^{1 - x + a}}v_{\mathrm{w}}^{x + b}a_{\mathrm{p}}^{{{1 + x + 2c} \mathord{\left/ {\vphantom {{1 + x + 2c} 2}} \right. } 2}} $$ (10) 其中：Kj、x、a、b和c均为待定系数，可以通过回归拟合获取，基准锯片组合锯切情况下koj = 1。
将P6中耦合效应带来的影响视为参数模型，根据表3可知P6模型为：
$$ {P_6} = 0.248{n^{0.379}}v_{\mathrm{w}}^{0.747}a_{\mathrm{p}}^{0.563} $$ (11) 则P7为：
$$ {P_7} = {K_7}{n^{0.379}}v_{\mathrm{w}}^{0.747}a_{\mathrm{p}}^{0.563} $$ (12) 通过多元非线性回归拟合对模型系数进行求解，可得K7为0.295，模型决定系数为98.6%，具有较高的拟合精度，因此可以认为模型具有较高的预测性能，这意味着可以采用少量样本实现组合锯切过程中功率的预测。该模型为组合锯切功率的预测提供了一个简单快速的解决方案。
3. 基于预测模型的锯切参数优化
3.1 优化模型目标函数和约束条件
锯切参数的选择直接关系加工用量，并对成本、能耗和效率等产生直接影响，选择合理的锯切参数是实现组合锯节能的关键。在实际生产过程中，提高组合锯的能量效率和缩短组合锯加工时间是实现其高效节能锯切中最为重要的2个部分。因此，本文以组合锯切过程中的锯切比能SEC和加工时间T共同最小为优化目标，对锯切参数进行优化。
$$ \min {F_{\mathrm{m}}}(n,{v_{\mathrm{f}}},{a_{\mathrm{p}}}) = \min [F(SEC) + F(T)] $$ (13) 其中，
$$ SEC = \frac{{{P_j}}}{{MRR}} = {K_j}{n^{0.379}}v_{\mathrm{w}}^{ - 0.253}a_{\mathrm{p}}^{ - 0.437} $$ (14) $$ T = \frac{1}{{1000}} \times \frac{L}{{{v_{\mathrm{w}}}}} \times \frac{H}{{{a_{\mathrm{p}}}}} $$ (15) $$ F = \frac{{f(x) - f{{(x)}_{\min }}}}{{f{{(x)}_{\max }} - f{{(x)}_{\min }}}} $$ (16) 式中：L和H分别为荒料长度和总锯切深度；MRR为材料去除率；F为将数据进行无量纲处理的转换函数；f(x)max和f(x)min分别为处理前单目标函数的最大值和最小值；x为优化决策变量。
锯切加工过程中的最优参数组合需满足锯机主轴转速、进给量、锯切深度等约束条件，另外，当锯切参数组合不理想时还会出现卡刀等状况，同样需要进行约束。
（1）nmin≤n≤nmax，nmin和nmax分别为锯机能够实现有效锯切的最小和最大转速；
（2）vw_min≤vw≤vw_max，vw_min和vw_max分别为锯切加工中锯机允许的最小和最大进给速度；
（3）ap_min≤ap≤ap_max，ap_min和ap_max分别为锯切过程中锯机允许的最小和最大锯切深度；
（4）为防止锯切过程中出现卡刀状况，根据现场调研结果及车间工人推荐参数值，对锯切参数做如下约束：
$$ \left\{ \begin{gathered} {v_{\mathrm{w}}} + {a_{\mathrm{p}}} \leqslant 14.45 \\ n \geqslant 370 \\ \end{gathered} \right. $$ (17) （5）Pj + Pidle≤ηmPmax，其中ηm为锯机传动效率。锯机主传动系统为带传动和齿轮传动的组合，因此取ηm为0.92，Pmax为锯机主电机额定功率，取55 kW，Pidle为主轴转速的二次函数，可通过实验进行测量与拟合：
$$ {P_{{\text{idle}}}} = 3.550 + 4.947 \times {10^{ - 5}}{n^2} - 0.013n $$ (18) 综上所述，选取能耗最大的4片组合锯切过程进行参数优化，约束条件为：
$$ {\text{s}}{\text{.t}}{\text{.}}\left\{ \begin{gathered} 370 \leqslant n \leqslant 410 \\ 1.45 \leqslant {v_{\text{w}}} \leqslant 9.45 \\ 2 \leqslant {a_{\text{p}}} \leqslant 14 \\ {v_{\mathrm{w}}} + {a_{\text{p}}} \leqslant 14.45 \\ {P_7} + {P_{{\text{idle}}}} \leqslant 50.6 \\ \end{gathered} \right. $$ (19) 3.2 改进粒子群算法
粒子群优化（particle swarm optimization，PSO）算法是基于群体的演化算法，源于对鸟类捕食行为的模拟，它在处理连续优化问题及组合优化问题上具有较好的性能，其基本原理如下[12]。假定有n个粒子运动在D维空间内运动，第i个粒子在搜索空间内的位置为xi = (xi1,xi2,···,xiD)，其运动速度为vi = (vi1,vi2,···,viD)，其个体的最优位置为pbest = (pbest1,pbest2,···,pbestD)，其种群最优位置为gbest = (gbest1,gbest2,···,gbestD)，则对于第k + 1次迭代，各粒子根据下列公式更新自己的位置和速度：
$$ \left\{ \begin{gathered} v_i^{k + 1} = \omega v_i^k + {c_1}{r_1}({p_{{\text{best}}}}_i^k - x_i^k) + {c_2}{r_2}({g_{{\text{best}}}}_i^k - x_i^k) \\ x_i^{k + 1} = x_i^k + v_i^{k + 1} \\ \end{gathered} \right. $$ (20) 式中：vik + 1和xik + 1分别为第k + 1次迭代时粒子i的飞行速度和位置；r1和r2为[0, 1]的随机数；ω为惯性权重因子；c1和c2分别为个体学习因子和全局学习因子。
传统的PSO算法收敛速度较快，但收敛精度低，容易陷入搜索停滞，导致优化结果较差。因此本文将传统的线性变化的惯性权重和加速因子替换为非线性变化的以获得更好的搜索性能：惯性因子采用指数递减策略[13]，学习因子采用正弦函数变化[14]。
$$ \omega = {\omega _{\min }}{({{{\omega _{\max }}} \mathord{\left/ {\vphantom {{{\omega _{\max }}} {{\omega _{\min }}}}} \right. } {{\omega _{\min }}}})^{{1 \mathord{\left/ {\vphantom {1 {(1 + {{{c_3}k} \mathord{\left/ {\vphantom {{{c_3}k} K}} \right. } K})}}} \right. } {(1 + {{{c_3}k} \mathord{\left/ {\vphantom {{{c_3}k} K}} \right. } K})}}}} $$ (21) $$ {c_1} = \frac{{{c_{12}} - {c_{11}}}}{2}\sin \left(\frac{{\text{π }}}{2} \cdot \frac{{{K \mathord{\left/ {\vphantom {K 2}} \right. } 2} - k}}{{{K \mathord{\left/ {\vphantom {K 2}} \right. } 2}}}\right) + \frac{{{c_{11}} + {c_{12}}}}{2} $$ (22) $$ {c_2} = \frac{{{c_{21}} - {c_{22}}}}{2}\sin \left(\frac{{\text{π }}}{{\text{2}}} \cdot \frac{{k - {K \mathord{\left/ {\vphantom {K 2}} \right. } 2}}}{{{K \mathord{\left/ {\vphantom {K 2}} \right. } 2}}}\right) + \frac{{{c_{21}} + {c_{22}}}}{2} $$ (23) 式中：ωmax和ωmin分别为惯性权重的初始值和最终值，分别取0.9和0.4；c3为调节参数，在本文中取10；c11和c12分别为c1的初始值和最终值；c21和c22分别为c2的初始值和最终值，根据现有的研究[15]，当c1在[0.50, 2.50]和c2在[1.00, 2.25]取值时，算法有较高的寻优能力；k为当前迭代次数；K为总迭代次数。
改进后的算法流程如图7所示。
图 7 改进粒子群算法求解流程Figure 7. The solving process of particle swarm optimization algorithm.本文采用改进粒子群算法求解锯切比能和锯切时间最小问题步骤如下。
（1）在参数约束条件的范围内随机生成种群初始位置和速度并设定算法参数；
（2）计算个体适应度pbest；
（3）若pbest<gbest，则将pbest作为新的历史最佳适应度，并更新其位置；
（4）根据式（21）～式（23）更新惯性权重和学习因子；
（5）根据式（20）更新粒子速度和位置；
（6）若满足k≥K，则停止寻优并输出gbest及其位置，否则转步骤（2）。
3.3 优化结果与分析
为验证算法的有效性，本实验在相同的参数设置下选用惯性权重和学习因子线性变化策略的改进算法（linear particle swarm optimization，LPSO）与非线性粒子群优化算法（nonlinear particle swarm optimization，NPSO）进行对比，所得结果列于表7。算法参数设置：粒子种群大小N = 100，最大迭代次数K=100，速度为位移的10%～20%。
表 7 优化结果对比分析Table 7. Comparative analysis of optimization results编号 方案 转速
n / (r·min−1)进给速度
vw / (m·min−1)锯切深度
ap / mmF 1 LPSO 378.78 6.22 8.22 0.043 NPSO 371.82 5.49 8.96 0.038 2 LPSO 375.24 5.91 8.54 0.039 NPSO 370.30 6.18 8.27 0.037 3 LPSO 378.16 5.69 8.69 0.043 NPSO 372.39 5.38 9.07 0.038 从表7可以得出，当转速为370.30 r/min、进给速度为6.18 m/min、锯切深度为8.27 m/min时，锯切比能和加工时间同时取得最小值，且本文所提的NPSO算法在收敛精度上优于传统的LPSO算法。结合组合锯性质与式（13）～式（15）可以得出，优化后的参数同样适用于其他组合锯切方式。
取锯切深度为相邻两锯片直径差的1/2，即200 mm，锯切长度为荒料长度2 500 mm，将优化后的参数与经验参数进行对比，所得结果列于表8。
表 8 优化解与经验解对比分析Table 8. Comparative analysis of optimal solution and empirical solution方法 转速
n / (r·min−1)进给速度vw / (m·min−1) 锯切深度
ap / mm锯切比能
SEC / (kJ·cm−3)加工时间
T / min优化 370.30 6.18 8.27 0.695 9.783 经验 410.00 5.45 8.00 0.757 11.468 根据表8可以得出，采用优化后的锯切参数进行锯切加工，能够提升8.2%的能量利用率，减少14.7%的加工时间，从长远来看，能够有效降低能耗和加工成本。
4. 结论
（1）采用基于组合锯中单锯片的单磨粒平均未变形切屑厚度的参数模型能够很好地预测不同锯片组合锯切过程中的功率，预测的误差在10%以内。
（2）采用改进后的参数模型能够实现锯切功率的少量样本预测，大大提高了模型预测的速度，并且具有较高的预测精度。
（3）采用惯性权重和学习因子非线性变化策略对PSO算法进行改进，以锯切比能和锯切时间最小为优化目标，以锯切参数为优化变量建立了优化模型，采用改进后的PSO算法进行模型求解，结果表明本文改进的算法具有较高的收敛精度，采用优化后的参数能够有效减少锯切过程的能源浪费。
-
图 2 单颗磨粒未变形切屑厚度变化示意图
Figure 2. Schematic diagram of the variation in undeformed chip thickness of a single abrasive particle
图 3 功率随锯切参数变化示意图
Figure 3. Schematic diagram of power variation with sawing parameters
图 7 改进粒子群算法求解流程
Figure 7. The solving process of particle swarm optimization algorithm.
表 1 锯切参数组合
Table 1. Sawing parameter combination
参数 取值 转速 n / (r·min−1) 380，395，410 进给速度 vw / (m·min−1) 3.45，4.45，5.45 锯切深度 ap / mm 4，6，8 
下载: 导出CSV
表 2 锯切能耗测量结果
Table 2. Measurement results of sawing energy consumption
编号 转速 n /
(r·min−1)进给速度
vw / (m·min−1)锯切
深度
ap / mm后3片组合
锯切功率
P6 / kW4片组合
锯切功率
P7 / kW1 380 3.45 4 12.74 15.20 2 380 4.45 4 15.66 17.33 3 380 5.45 4 18.89 21.56 4 380 3.45 6 16.22 19.11 5 380 4.45 6 19.50 22.92 6 380 5.45 6 22.59 27.04 7 380 3.45 8 19.72 22.74 8 380 4.45 8 22.97 26.97 9 380 5.45 8 26.81 31.96 10 395 3.45 4 13.29 15.57 11 395 4.45 4 15.74 18.84 12 395 5.45 4 18.90 22.87 13 395 3.45 6 16.93 19.58 14 395 4.45 6 19.69 23.32 15 395 5.45 6 23.44 27.52 16 395 3.45 8 19.59 22.80 17 395 4.45 8 23.31 27.73 18 395 5.45 8 27.84 32.62 19 410 3.45 4 13.51 16.58 20 410 4.45 4 15.96 19.29 21 410 5.45 4 18.91 22.42 22 410 3.45 6 16.84 19.79 23 410 4.45 6 19.78 23.99 24 410 5.45 6 23.47 27.94 25 410 3.45 8 19.83 23.32 26 410 4.45 8 23.59 28.35 27 410 5.45 8 28.38 35.44
下载: 导出CSV
表 3 P6模型拟合系数
Table 3. Fitting coefficients of the P6 model
系数 Beta1 Beta2 Sig VIF kcp6 0.144 <0.001 K6 0.248 0.033 x 0.543 <0.001 1.000 a 0.078 0.055 <0.001 1.000 b 0.204 0.655 <0.001 1.000 c −0.210 0.750 <0.001 1.000 R2 99.4% <0.001 DW 2.355 RMSE 0.017
下载: 导出CSV
表 4 P7模型拟合系数
Table 4. Fitting coefficients of the P7 model
系数 Beta1 Beta2 Sig VIF kcp7 0.171 <0.001 K7 0.027 <0.001 x 0.543 <0.001 1.000 a −0.312 0.109 <0.001 1.000 b 0.228 0.660 <0.001 1.000 c −0.205 0.737 <0.001 1.000 R2 99.0% <0.001 DW 1.808 RMSE 0.022
下载: 导出CSV
表 5 P6模型对比分析
Table 5. Comparative analysis of the P6 model
编号 转速 n
/ (r·min−1)进给速度vw /
(m·min−1)锯切深度ap / mm P预测 / kW P实测 / kW η / % 1 370 3.45 8 18.97 18.40 3.10 2 385 4.45 6 19.80 20.97 5.58 3 400 5.45 4 18.61 19.29 3.53
下载: 导出CSV
表 6 P7模型对比分析
Table 6. Comparative analysis of the P7 model
编号 转速 n
/ (r·min−1)进给速度vw /
(m·min−1)锯切深度ap / mm P预测 / kW P实测 / kW η / % 1 370 3.45 8 21.53 23.25 7.40 2 385 4.45 6 22.94 24.03 4.54 3 400 5.45 4 21.95 22.95 4.35
下载: 导出CSV
表 7 优化结果对比分析
Table 7. Comparative analysis of optimization results
编号 方案 转速
n / (r·min−1)进给速度
vw / (m·min−1)锯切深度
ap / mmF 1 LPSO 378.78 6.22 8.22 0.043 NPSO 371.82 5.49 8.96 0.038 2 LPSO 375.24 5.91 8.54 0.039 NPSO 370.30 6.18 8.27 0.037 3 LPSO 378.16 5.69 8.69 0.043 NPSO 372.39 5.38 9.07 0.038
下载: 导出CSV
表 8 优化解与经验解对比分析
Table 8. Comparative analysis of optimal solution and empirical solution
方法 转速
n / (r·min−1)进给速度vw / (m·min−1) 锯切深度
ap / mm锯切比能
SEC / (kJ·cm−3)加工时间
T / min优化 370.30 6.18 8.27 0.695 9.783 经验 410.00 5.45 8.00 0.757 11.468
下载: 导出CSV
-
[1] TURCHETTA S. Cutting force and diamond tool wear in stone machining [J]. The International Journal of Advanced Manufacturing Technology,2012,61(5):441-448. [2] POLINI W, TURCHETTA S. Force and specific energy in stone cutting by diamond mill [J]. International Journal of Machine Tools and Manufacture,2004,44(11):1189-1196. doi: 10.1016/j.ijmachtools.2004.04.001 [3] 黄国钦, 徐西鹏. 基于锯切弧区切向力分布的功率消耗模型 [J]. 机械工程学报,2011,47(21):170-176. doi: 10.3901/JME.2011.21.170HUANG Guoqin, XU Xipeng. Establishment of power model for circular sawing based on tangential force distribution at the contact zone [J]. Chinese Journal of Mechanical Engineering,2011,47(21):170-176. doi: 10.3901/JME.2011.21.170 [4] HUANG G, ZHANG M, HUANG H, et al. Estimation of power consumption in the circular sawing of stone based on tangential force distribution [J]. Rock Mechanics and Rock Engineering,2018,51(4):1249-1261. doi: 10.1007/s00603-017-1380-2 [5] 张昆, 田业冰, 丛建臣, 等. 基于动态惯性权重粒子群算法的磨削低能耗加工方法 [J]. 金刚石与磨料磨具工程,2021,41(1):71-75.ZHANG Kun, TIAN Yebing, CONG Jianchen, et al. Reduce grinding energy consumption by modified particle swarm optimization based on dynamic inertia weigh [J]. Diamond & Abrasives Engineering,2021,41(1):71-75. [6] 陈行政, 李聪波, 吴磊, 等. 面向能耗的多刀具孔加工刀具直径及工艺参数集成优化模型 [J]. 机械工程学报,2018,54(15):221-231. doi: 10.3901/JME.2018.15.221CHEN Xingzheng, LI Congbo, WU Lei, et al. Integrating optimization of cutter diameter and cutting parameters for energy-aware multi-tool hole machining [J]. Chinese Journal of Mechanical Engineering,2018,54(15):221-231. doi: 10.3901/JME.2018.15.221 [7] 黄国钦, 黄辉, 郭桦, 等. 串珠绳锯切花岗石过程中锯切参数对锯切力和能耗的影响 [J]. 机械工程学报,2009,45(3):234-239. doi: 10.3901/JME.2009.03.234HUANG Guoqin, HUANG Hui, GUO Hua, et al. Influences of sawing parameters on forces and energy in wire sawing of granite [J]. Journal of Mechanical Engineering,2009,45(3):234-239. doi: 10.3901/JME.2009.03.234 [8] KONSTANTY J. Theoretical analysis of stone sawing with diamonds [J]. Journal of Materials Processing Technology,2002,123(1):146-154. doi: 10.1016/S0924-0136(02)00071-7 [9] LI K, LIAO W. Modelling of ceramic grinding processes part I. Number of cutting points and grinding forces per grit [J]. Journal of Materials Processing Technology,1997,65(1/2/3):1-10. [10] ZHOU J, WANG K, ZHANG J, et al. Rock breakage and tools performance during rock processing by multidiameter combination saw with different diameters [J]. Rock Mechanics and Rock Engineering,2022,55(7):4459-4476. doi: 10.1007/s00603-022-02824-9 [11] 周京国. 塔形组合式金刚石圆锯片锯切特性研究[D]. 济南: 山东大学, 2022.ZHOU Jingguo. Sawing performance of tower combined diamond circular saw blade[D]. Jinan: Shandong University, 2022. [12] 帅茂杭, 熊国江, 胡晓, 等. 基于改进多目标骨干粒子群算法的电力系统环境经济调度 [J]. 控制与决策,2022,37(4):997-1004.SHUAI Maohang, XIONG Guojiang, HU Xiao, et al. Economic emission dispatch of power system based on improved bare-bone multi-objective particle swarm optimization algorithm [J]. Control and Decision Making,2022,37(4):997-1004. [13] 陈贵敏, 贾建援, 韩琪. 粒子群优化算法的惯性权值递减策略研究 [J]. 西安交通大学学报,2006(1):53-56,61.CHEN Guimin, JIA Jianyuan, HAN Qi. Study on the strategy of decreasing inertia weight in particle swarm optimization algorithm [J]. Journal of Xi'an Jiaotong University,2006(1):53-56,61. [14] 贾会群, 魏仲慧, 何昕, 等. 基于改进粒子群算法的路径规划 [J]. 农业机械学报,2018,49(12):371-377.JIA Huiqun, WEI Zhonghui, HE Xin, et al. Path Planning Based on Improved Particle Swarm Optimization Algorithm [J]. Journal of Agricultural Machinery,2018,49(12):371-377. [15] 毛开富, 包广清, 徐驰. 基于非对称学习因子调节的粒子群优化算法 [J]. 计算机工程,2010,36(19):182-184.MAO Kaifu, BAO Guangqing, XU Chi. Particle swarm optimization algorithmbasedon non-symmetric learning factor adjusting [J]. Computer Engineering,2010,36(19):182-184. -
下载:
点击查看大图
计量
- 文章访问数: 667
- HTML全文浏览量: 328
- PDF下载量: 21
- 被引次数: 0
邮件订阅
RSS
